Regressziószámítás

A statisztikában a regressziószámítás vagy regresszióanalízis során két vagy több véletlen változó között fennálló kapcsolatot modellezzük. A regressziós modell tulajdonságai alapján megkülönböztethetünk lineáris és nemlineáris regressziót, az adataink alapján pedig idősor, keresztmetszeti, és panel regresszióanalízist.

A feladat

A regresszió feladata két vagy több valószínűségi változó közötti $y=f(x_1,x_2,\dots ,x_n)$ függvénykapcsolat meghatározása. A változókat reprezentáló (n+1) dimenziós $P(y;x_1,x_2,\dots ,x_n)$ vektor koordinátáira kapott m számú $P_1,P_2,\dots ,P_m$ mérési adatból meg kell határozni egy, a vizsgált jelenséget leíró, jól kezelhető függvényt: $y=f(x_1,x_2,\dots ,x_n)=f(X)$, amelynek az $X_k=(x_1,x_2,\dots ,x_n{)}_k$ helyeken felvett ${\hat{y}}_k=f(X_k)$ értékei

• vagy megegyeznek a megfelelő mért értékekkel: ${\hat{y}}_k=y_k$ - (interpoláció),
• vagy az $e_k=(y_k-{\hat{y}}_k)$ eltérések valamilyen minimum-feltételnek eleget tesznek (regresszió).

Az eltérések mértékét többféleképpen lehet megadni. Leggyakrabban a hibaértékek $e_k$ eltérések : $\sum _{i=1}^m{e}_k^2$ négyzetösszegének minimumát követeljük meg. (l.: legkisebb négyzetek módszere). A vizsgált jelenség természete szabja meg a közelítésre alkalmas függvény típusát. Eszerint megkülönböztetünk lineáris és nemlineáris regressziót. A kapcsolt változók száma szerint ugyancsak eltérnek a modellek. Ilyen értelemben beszélünk két-, három- stb. változós regresszióról.

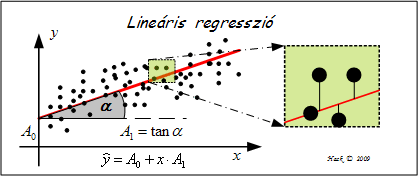
Lineáris regresszió

Az általános lineáris modell az

$\hat{y}=A_0+A_1{x}_1+A_2{x}_2+\dots +A_n{x}_n$

függvény $A_i$ együtthatóinak meghatározását követeli meg. (Többváltozós lineáris regresszió.) A leggyakoribb kétváltozós lineáris modell a síkon derékszögű koordináta-rendszerben pontokkal ábrázolható adathalmazra $\hat{y}=A_{1}x+A_0$ egyenletű egyenes illesztését írja elő. Ezt az egyenest szokás trend-vonalnak, az egyenlet $A_1$ együtthatóját trendnek (meredekség, tendencia), $A_0$ konstansát tengelymetszetnek nevezni. Az együtthatók becslésére alkalmazott eljárások:

• a legkisebb négyzetek módszere (angolul Ordinary Least Squares – OLS)
• az általánosított legkisebb négyzetek módszere (Generalized Least Squares – GLS)
• az általánosított momentumok módszere (Generalized Method of Moments – GMM)
• a legnagyobb valószerűség módszere (Maximum Likelihood estimation – ML).

Nemlineáris regresszió

Nemlineáris regressziószámítást akkor alkalmaznak, ha a modell nemlineáris. Az ilyenkor alkalmazható linearizáló módszer abból áll, hogy az eredeti $(y;x_1,\dots )$ változók helyett, velük összefüggő, de egymással lineáris kapcsolatban lévő $(Y;X_1,\dots )$ változókat vezetünk be.

Például az $y=A\cdot e^{Bx}$ formulából az $X=x;Y=\ln y$ helyettesítésekkel az $Y=\ln A+B\cdot X$ lineáris kapcsolat adódik. Ennek(a,b) együtthatóiból az eredeti formula konstansai adódnak: $A=e^a;B=b$.

Regresszió. Gyakorlati alkalmazások

• Kehl Dániel-Sipos Béla. Excel parancsfájlok felhasználása a statisztikai elemzésekben. Oktatási segédlet. Gyakorlati alkalmazások. OSZK-MEK (PDF és XLSM) (magyar nyelven). (Hozzáférés: 2022. március 1.)