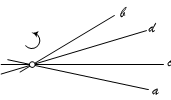
Kettősviszony

A kettősviszony egy egyenes (pontsor) négy pontjára, illetve egy sugársor négy elemének kölcsönös elhelyezkedésére jellemző viszonyszám. A projektív geometria fontos alapfogalma: centrális vetítéskor a távolságok és a szögek változnak, a kettősviszony megmarad (invariáns). Ezt Papposz egyik fontos tétele biztosítja.

Értelmezése

Az $A,B,C,D$ pontnégyes $(ABCD)$ kettősviszonya az $(ABC)$ és $(ABD)$ egyszerű- vagy osztóviszonyok hányadosa (viszonya):

• ($ABCD)=(ABC):(ABD)$

A három pont viszonylagos helyzetét jellemző osztóviszonyt szakaszok hányadosa definiálja:

• $(ABC)=\frac{AC}{CB}$ ,
• $(ABD)=\frac{AD}{DB}$ .

A pontnégyes és a sugárnégyes kettősviszonya:

• $(ABCD)=\frac{AC}{CB}:\frac{AD}{DB}$ ,

• $(abcd)=\frac{\sin ac}{\sin cb}:\frac{\sin ad}{\sin db}$ .

A formulákban szereplő szakaszok és szögek irányítottak, előjelesek. Néhány példa az osztóviszonyra: $(ABF)=3:3=1$ (felezőpont), $(ABG)=2:4=0,5$ (harmadoló pont, A-hoz közelebbi), $(ABH)=4:2=2$ (harmadoló pont, B-hez közelebbi), $(ABM)=(-2):8=-0,25$ $(ABN)=8:(-2)=-4$ $(ABB)=6:0=+\mathrm{\infty }$ $(AAB)=6:(-6)=-1$ $(ABA)=0:6=0$ Néhány példa a kettősviszonyra: $(ABFG)=1:0,5=2$ $(ABGH)=0,5:2=0,25$ $(ABGN)=0,5:(-4)=-0,125$ $(ABFN)=1:(-4)=-0,25$ $(ABHN)=2:(-4)=-0,5$ $(ABNH)=-4:2=-2$.

Harmonikus négyes

Különös fontosságú az olyan pontnégyes, amelynek kettősviszonya $(ABXY)=-1$. Ez csak úgy lehet, hogy X és Y közül az egyik pont az AB szakaszon, másik azon kívül helyezkedik el, s az osztóviszonyokra pedig teljesül: $(ABX)=-(ABY).$

Papposz tétele

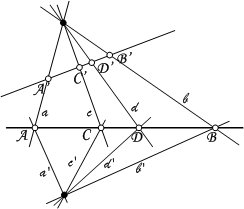
Ha az egy pontra illeszkedö $a,b,c,d$ egyenesek egy, a közös pontjukra nem illeszkedő egyenest rendre az $A,B,C,D$ pontokban metszenek, akkor $(ABCD)=(abcd).$ A tétel egyszerű következménye, hogy ha két egyenest metsz a sugársor, akkor az egyik egyenesen a metszéspontok kettősviszonya a másik egyeneseken keletkező vetületüknek a kettősviszonyával egyezik: $(ABCD)=(A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }).$ Hasonló összefüggés igazolható a közös egyenesre illeszkedő sugársorok négyeseire: $(abcd)=(a^{\prime }{b}^{\prime }{c}^{\prime }{d}^{\prime })$.

Irodalom

• Hajós György, Bevezetés a geometriába, Tankönyvkiadó, Budapest, 1960.