Felhajtóerő (hidrosztatika)

Felhajtóerő változása változó sűrűségű folyadékban. A jobb oldali csészében víz van, a bal oldaliban etanol

A nyugvó folyadék és gáz a benne lévő testre felfelé irányuló erővel hat. Ezt az erőt felhajtóerőnek nevezzük.

A felhajtóerő függ

• a test folyadékba bemerülő részének térfogatától;
• a folyadék sűrűségétől.

A felhajtóerő nagysága nem függ a test anyagától. Megállapítható, hogy a felhajtóerő nem csak a folyadékba, hanem a gázba merülő testre is hat.

Arkhimédész törvénye

Minden folyadékba vagy gázba merülő testre felhajtóerő hat. A felhajtóerő egyenlő nagyságú a test által kiszorított folyadék vagy gáz súlyával. Ez Arkhimédész törvénye. A felhajtóerő nagyságát a kiszorított folyadék térfogatának és sűrűségének ismeretében ki is számolhatjuk. A felhajtóerő a hidrosztatikai nyomásból származtatható. A felhajtóerő meghatározható úgy, hogy kiszámítjuk a kiszorított folyadék tömegét és abból következtetünk a kiszorított folyadék súlyára, illetve a felhajtóerőre. Arkhimédész törvényét az alábbi gondolatkísérlettel lehet igazolni: Vegyünk egy tetszőleges szabályos vagy szabálytalan alakú szilárd testet. Nyugalomban lévő folyadékban gondolatban jelöljünk ki egy olyan zárt felületet, mely megegyezik a szilárd test felületével (tehát a test és a folyadékrész térfogata egyenlő). Erre a folyadékrészre a súlya hat, mely feltételünk szerint egyensúlyban van a környezetével. Ha a folyadékrészt helyettesítjük a szilárd testtel, a megmaradt folyadék ugyanolyan erővel hat a felületére, mint az előzőekben, tehát a felhajtóerő a test térfogatával egyenlő térfogatú folyadék súlyával egyezik meg, a felhajtóerő támadási pontja pedig a folyadékrész tömegközéppontjában lesz.

Úszás

Vegyünk egy ${\rho }_f$ sűrűségű folyadékba merülő, $V$ térfogatú, $\rho$ sűrűségű testet. A test súlya: $G_{test}=\rho Vg$. Arkhimédész törvénye miatt rá $F_{felh.}=G_f={\rho }_f{V}^{\prime }g$ nagyságú felhajtóerő hat. ($G_f$ a folyadék felhajtóereje, $V^{\prime }$ a test térfogatának folyadékba merülő része.) A test akkor van egyensúlyban, ha a két erő kiegyenlíti egymást, $G_{test}=F_{felh.}$. Ekkor a test a folyadék felszínén lebeg. Ha a felhajtóerő nagyobb, mint a test súlya, akkor a test emelkedik, ha kisebb, akkor a test süllyed. Az egyensúlynak azonban nemcsak az a feltétele, hogy az úszó test súlya megegyezzék a felhajtóerővel, hanem az is, hogy a két erő egy függőlegesbe essék. Ha ugyanis ez nem áll fenn, a testre nyomaték hat, melynek nagysága, ha a két erő támadáspontját összekötő egyenes szakasz vízszintes vetülete $\mathrm{\Delta }y$:

$M=G_{test}\mathrm{\Delta }y.$

A víz felszínén úszó testek esetén a folyadék felszínének neve: úszósík. A testnek az úszósíkban lévő szelvénye az úszófelület vagy vízvonalfelület, az úszófelületet határoló síkidom a vízvonal. Megjegyzendő, hogy az említett jellemzők függenek a hajó alakján és önsúlyán kívül a tehertől, sőt attól is, hogy a hajó édesvízbe vagy tengervízbe merül.

A felhajtóerő és a hidrosztatikai nyomás

Egy $\rho$ sűrűségű folyadékban, $h$ mélységben a hidrosztatikai nyomás értéke: $p=\rho \cdot g\cdot h,$ ahol $g$ a földi nehézségi gyorsulás. A folyadékba helyezett testre tehát a test különböző mélységben lévő pontjainál különbözik a hidrosztatikai nyomás nagysága. Ahogy az ábráról is látszik, a nyomáskülönbségből származó erő felfelé hat. Az erők különbségének kifejezésében a kiszorított folyadék sűrűsége ($\rho$), test magassága ($h$), és alapterülete $A$ szerepel. A magasság és az alapterület szorzata megegyezik a test térfogatával: $V=h\cdot A$. A felhajtóerő nagysága ezért a kiszorított folyadék súlyával egyenlő: $F_f=\rho \cdot g\cdot h\cdot A=\rho \cdot g\cdot V.$ A felhajtóerő tehát abból származik, hogy a folyadékban a hidrosztatikai nyomás függ a mélységtől.

Stabilitás

Metacentrum. M₀=kezdeti metacentrum, M_φ=φ dőlésszöghöz tartozó metacentrum

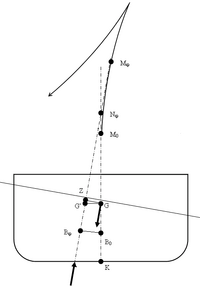
Az úszó test egyensúlyához a fentiek szerint a felhajtóerő és a test súlyának egyenlősége és az kell, hogy a két erő támadáspontja egy egyenesbe essen. Ha az úszó testet egy forgatónyomaték kitéríti (például oldalirányú szél a vitorlás hajót), akkor az új helyzetbe került test felhajtóereje és súlya nem esik egy egyenesbe, az ebből származó nyomaték egyensúlyt tart a kitérítő nyomatékkal. Az úszási tengely és a felhajtóerőnek a kitérített helyzetbeni egyenesének metszéspontja a metacentrum. A test egyensúlyi helyzete akkor stabil, ha a metacentrum a test tömegközéppontja felett helyezkedik el. Ha a két pont egybeesik, az egyensúly közömbös (például üres ledugózott palack esetében), ha a metacentrum a tömegközéppont alatt helyezkedik el, az egyensúly labilis, a legkisebb kitérítésre a test felfordul. A tömegközéppont és a metacentrum távolsága a metacentrikus magasság a stabilitásra jellemző szám. A metacentrikus magasság nem állandó érték, a kitérés szögétől függően változik. A kezdeti metacentrikus magasság, vagyis kis kitérésekre az alábbi képlettel számítható:

$h_m=\frac{I_0}{V}-e,$

ahol

• $h_m$ a metacentrikus magasság,
• $I_0$ az úszófelület másodrendű nyomatéka az elfordulás y tengelyére, az úszófelület, az úszó test és a folyadékfelszín metszéséből származó síkidom,
• $V$ a kiszorított folyadéktérfogat,
• $e$ a test tömegközéppontja és a kiszorított folyadéktérfogat tömegközéppontja közötti távolság nyomatékmentes helyzetben.

A metacentrikus magasság szokásos értékei különböző hajóknál

Hajófajta	Metacentrikus magasság hm [m]
Teherhajók	0,6…0,9
Személyszállító hajók	0,45..0,6
Vitorlás hajók	0,9…1,5
Hadihajók	0,75..1,3

Kezdeti metacentrikus magasság levezetése

Kezdeti metacentrikus magasság
M - metacentrum
S - tömegközéppont
F - felhajtóerő

Kezdeti metacentrikus magassághoz
Kék vonal - vízvonal
Sárga idom - úszófelület

Kis Δφ szögelfordulásnál igaz, hogy

$\mathrm{\Delta }\varphi \approx \sin \mathrm{\Delta }\varphi \approx \mathrm{t}\mathrm{g}\mathrm{\Delta }\varphi$ és

$\cos \mathrm{\Delta }\varphi \approx 1.$

A kibillent helyzetben az ábrák szerint egy dx vastagságú réteg kiszorított víztérfogata úgy változik, hogy jobboldalt a kék háromoldalú hasábbal megnő, bal oldalon pedig a zöld háromoldalú hasábbal csökken. A felhajtóerő abszolút értéke változatlan marad (kis kitérések esetén a két háromoldalú hasáb térfogata azonos), de támadáspontja jobbra tolódik és hatásvonala az úszási tengelyt az M metacentrumban metszi. A dx vastagságú réteget eredeti helyzetébe visszaállítani akaró nyomaték:

$dM=2g\rho \frac{y^2\mathrm{\Delta }\varphi }{2}\frac{2}{3}ydx,$

az egész hajó nyomatéka pedig:

$M=2g\rho \mathrm{\Delta }\varphi \frac{2}{3}\int y^{3}dx.$

Ezzel a nyomatékkal a teljes V térfogat felhajtóerejének nyomatéka egyenlő:

$M=\mathrm{\Delta }yVg\rho$

és így írható:

$\mathrm{\Delta }y=\mathrm{\Delta }\varphi \frac{\frac{2}{3}\int y^{3}dx}{V}.$

A fenti kifejezés számlálója nem más, mint az úszófelület másodrendű nyomatéka az x tengelyre:

$I_0=\underset{0}{\overset{l}{\int }}\frac{1}{12}(2y{)}^{3}dx=\frac{2}{3}\underset{0}{\overset{l}{\int }}{y}^{3}dx,$

$\mathrm{\Delta }y=(e+h_m)\mathrm{\Delta }\varphi$

így

$h_m=\frac{I_0}{V}-e.$

További információk

• Letölthető interaktív flash szimuláció a felhajtóerő tanulmányozásához magyarul. Elérés: magyarázó oldalon át Archiválva 2012. november 20-i dátummal a Wayback Machine-ben vagy közvetlenül a PhET-től
• Letölthető interaktív flash szimuláció a folyadékba merülő testek sűrűségének tanulmányozásához a PhET-től magyarul

Források

• Pattantyús: Gépész- és villamosmérnökök kézikönyve 2. kötet. Műszaki Könyvkiadó, Budapest, 1961.
• Dr. Gruber József-Blahó Miklós: Folyadékok mechanikája. Hatodik kiadás. Tankönyvkiadó, Budapest, 1965.
• Willi Bohl: Műszaki áramlástan. Műszaki könyvkiadó, Budapest, 1983. ISBN 9631044831