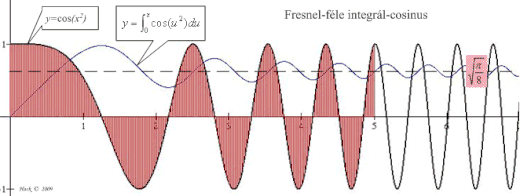
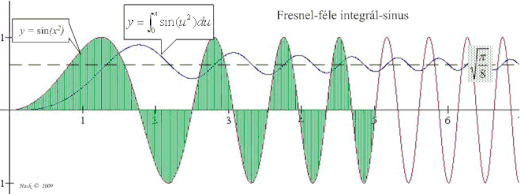
Fresnel-integrál

A Fresnel-integrálok az $x\to C(x)$ és $x\to S(x)$ leképezésekkel adott transzcendens valós-valós függvények, ahol

$C(x)=\underset{0}{\overset{x}{\int }}\cos (u^2)du,S(x)=\underset{0}{\overset{x}{\int }}\sin (u^2)du.$

$C(x)$ illetve $S(x)$ az $y=\cos (x^2)$ és az $y=\sin (x^2)$ függvény területfüggvénye (x=0 kezdő abszcisszától).

Leírásuk

A Fresnel-integrálok nem írhatók fel elemi függvényekkel zárt analitikus alakban. A helyettesítési érték kiszámítására a következő, minden $x\in \mathbb{ℝ}$ helyen konvergens hatványsorok alkalmasak:

$S(x)=\frac{x^3}{3\cdot 1!}-\frac{x^7}{7\cdot 3!}+\frac{x^{1}1}{11\cdot 5!}\mp \dots +(-1{)}^n\frac{x^{4n+3}}{(4n+3)(2n+1)!},$

$C(x)=\frac{x}{1\cdot 0!}-\frac{x^5}{7\cdot 2!}+\frac{x^9}{9\cdot 4!}\mp \dots +(-1{)}^n\frac{x^{4n+1}}{(4n+1)(2n)!}.$

A függvények csökkenő amplitúdóval és hullámhosszal oszcillálnak a $+\mathrm{\infty }$ -ben vett határértékük körül (nem periodikusak!):

$\underset{0}{\overset{\mathrm{\infty }}{\int }}\cos u^{2}du=\underset{0}{\overset{\mathrm{\infty }}{\int }}\sin u^{2}du=\sqrt{\frac{\pi }{8}}.$

A függvénygörbék egy transzponált alakja az elméleti vizsgálatokban használt normalizált alak:

$S_o(x)=\underset{0}{\overset{x}{\int }}\sin ({\frac{\pi u}{2}}^2)du,C_o(x)=\underset{0}{\overset{x}{\int }}\cos ({\frac{\pi u}{2}}^2)du,$

melyek a $\underset{x\to +\mathrm{\infty }}{\lim }{C}_o(x)=\underset{x\to +\mathrm{\infty }}{\lim }{S}_o(x)=\frac{1}{2}$ érték körül oszcillálnak.

Normalizált Fresnel-integrálok, So(x) és Co(x).

Alkalmazása

A függvényeket Augustin-Jean Fresnel (1788-1827) francia fizikus alkalmazta a fényinterferencia vizsgálatok matematikai elemzésénél. E vizsgálatok a fénynek Christiaan Huygens (1629-1695) holland fizikus által kidolgozott hullámtermészetét igazolták. Vele egy időben és tőle függetlenül hasonló sikeres kísérleteket végzett Thomas Young (1773-1829) angol orvos. Az út-/vasútépítésben fontos átmeneti ív, a klotoid (Cornu-spirál, Euler-spirál) paraméteres egyenletrendszerét a két Fresnel-integrál megfelelő transzformációjával lehet megadni:

$\{\begin{array}{l}x(t)=k\cdot C(t)\\ y(t)=k\cdot S(t)\end{array}$

Irodalom

• Reinhardt–Soeder: SH atlasz-Matematika (Springer-Verlag, 1993)
• Szász Pál: A differenciál- és integrálszámítás elemei (Közoktatásügyi Kiadóvállalat, 1951)
• Bronstein–Szemengyajev: Matematikai zsebkönyv. Műszaki könyvkiadó, Budapest, 1987. ISBN 963 1053091
• Pattantyús: Gépész- és Villamosmérnökök Kézikönyve 1. kötet. Műszaki Könyvkiadó, Budapest, 1961.