Inverz hiperbolikus függvények

A trigonometrikus és hiperbolikus függvények, illetve ezek inverzei

Az arsh (area hiperbolikus szinusz) függvény

Az arch (area hiperbolikus koszinusz) függvény

Az arth (area hiperbolikus tangens) függvény

Az arcth (area hiperbolikus kotangens) függvény

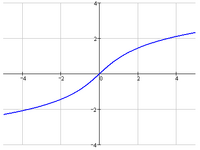
Az inverz hiperbolikus függvények – más néven area hiperbolikus függvények – a hiperbolikus függvények inverzei. Az area név onnan ered, hogy értékük – ha valós és nemnegatív – megegyezik a derékszögű koordináta-rendszerben felrajzolt $x^2-y^2=1$ hiperbola, valamint két – az argumentumtól függő – origón átmenő, ellentett meredekségű egyenes által határolt terület nagyságával.

Megjegyzés: Ugyanez az inverz trigonometrikus függvényekről is elmondható, azzal a különbséggel, hogy ott az $x^2+y^2=1$ egyenletű egységkör szerepel. Az inverz trigonometrikus függvények esetében azonban (a körívhossz és körcikkterület arányossága miatt) a függvényértékre nemcsak mint területre, hanem mint ívhosszra is gondolhatunk, ezért jelölik őket arc (arcus, ív) előtaggal.

Jelölésük

Az area hiperbolikus szinusz példáján bemutatva:

• A legelterjedtebb jelölés az arsh illetve az arsinh.
• A számítástechnikában leggyakrabban asinh-val jelölik.
• Az sh^-1 jelölés szintén használatos, de ügyelni kell arra, hogy a -1 ne legyen összetéveszthető a reciprokképzéssel.
• Az arcsinh forma is gyakori, annak ellenére, hogy az arc rövidítés az arcus, azaz ív szó helyett áll, a hiperbolikus függvények pedig területnagysághoz kapcsolódnak, ívhosszhoz nem. Ezért helyesebb az ar jelölést használni, ami az area, azaz a terület szóból ered.

Kiszámításuk

Az area-függvények megkaphatók bizonyos irracionális kifejezések logaritmusaként:

$\mathrm{arsh}x=\ln (x+\sqrt{x^2+1})$

$\mathrm{arch}x=\ln (x+\sqrt{x^2-1})=\ln (x+\sqrt{x-1}\sqrt{x+1})$

$\mathrm{arth}x=\frac{1}{2}\ln \left(\frac{1+x}{1-x}\right)$

$\mathrm{arcsch}x=\ln (\sqrt{1+\frac{1}{x^2}}+\frac{1}{x})$

$\mathrm{arsch}x=\ln (\sqrt{\frac{1}{x}-1}\sqrt{\frac{1}{x}+1}+\frac{1}{x})$

$\mathrm{arcth}x=\frac{1}{2}\ln \left(\frac{x+1}{x-1}\right)$

A fenti képletek a komplex számok körében is érvényesek. Ebben az esetben ügyelni kell arra, hogy a logaritmus és a négyzetgyök főértékével (principálisával) számoljunk és akkor a függvényérték esetén is a főértéket kapjuk. Erre azért van szükség, mert az area-függvények a komplex számok halmazán nem egyértékűek, hiszen a komplexek között az exponenciális függvény periodikus.

Tulajdonságaik

Areasinus hyperbolicus és areacosinus hyperbolicus

• A valós areasinus hyperbolicus minden valós számra értelmezett. A valós areacosinus hyperbolicus csak az $1\le x<+\mathrm{\infty }$ számokra értelmes.
• A valós areasinus hyperbolicus értékkészlete a valós számok halmaza. A valós areacosinus hyperbolicus értékkészlete a nemnegatív számok halmaza.
• Szigorúan monoton növő függvények.
• Nem periodikusak. A valós areasinus hyperbolicus páratlan függvény.
• A valós areasinus hyperbolicusnak inflexiós pontja van az $x=0$ helyen.
• A valós areasinus hyperbolicus nullhelye $x=0$-ben, a valós areacosinus hyperbolicusé $x=1$-ben van.

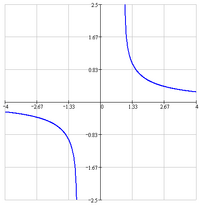
Areatangens hyperbolicus és areacotangens hyperbolicus

• A valós areatangens hyperbolicus értelmezett a $-1<x<1$ szakaszon. Nullhelye a nullában van, ami inflexiós pont is. A valós areacotangens hyperbolicus értelmezési tartománya két félegyenes uniója: $-\mathrm{\infty }<x<-1\cup 1<x<\mathrm{\infty }$.
• A valós areatangens hyperbolicus értékkészlete a valós számok halmaza. A valós areacotangens hyperbolicus értékkészlete a valós számok halmaza, kivéve a nullát.
• A valós areatangens hyperbolicus szigorúan monoton nő. A valós areacotangens hyperbolicus szigorúan monoton csökken a $-\mathrm{\infty }<x<-1$ és a $1<x<\mathrm{\infty }$ tartományon is.
• Nem periodikus, páratlan függvények.
• A valós areatangens hyperbolicus aszimptotái: $x=1:f(x)\to \mathrm{\infty }\text{ ha }x\to 1$, és $x=-1:f(x)\to -\mathrm{\infty }\text{ ha }x\to -1$. A valós areacotangens hyperbolicus aszimptotái: $y=0:f(x)\to 0\text{ ha }x\to \pm \mathrm{\infty }$
• Pólusaik vannak az $x=\pm 1$ helyen.

Areasecans hyperbolicus és areacosecans hyperbolicus

• A valós areasecans hyperbolicus értelmezett az $0<x\le 1$ számokon. A valós areacosecans hyperbolicus értelmezési tartománya $-\mathrm{\infty }<x<+\mathrm{\infty };x\ne 0$.
• A valós areasecans hyperbolicus értékkészlete: $0\le f(x)<+\mathrm{\infty }$. A valós areacosecans hyperbolicus értékkészlete: $-\mathrm{\infty }<f(x)<+\mathrm{\infty };f(x)\ne 0$.
• A valós areasecans hyperbolicus szigorúan monoton csökken. A valós areacosecans hyperbolicus szigorúan monoton csökken a negatív, illetve a pozitív számokon.
• Nem periodikusak. A valós areacosecans hyperbolicus páratlan függvény.
• A valós areasecans hyperbolicus inflexiós pontja $x=\frac{1}{2}\sqrt{2}$.

Nullhelye $x=1$.

• A valós areasecans hyperbolicus aszimptotája $f(x)\to 0$  ; $x\to +1$. valós areacosecans hyperbolicus aszimptotája $f(x)\to 0$  ; $x\to \pm \mathrm{\infty }$

Algebrai összefüggések

Teljesülnek a következők:

$\mathrm{arsh}(x)=\mathrm{sgn}(x)\cdot \mathrm{arcosh}\left(\sqrt{x^2+1}\right)$

ahol $\mathrm{sgn}$ a szignumfüggvény. Ha $x\ge 1$, akkor:

$\mathrm{arch}(x)=\mathrm{arsh}\left(\sqrt{x^2-1}\right)$

$\begin{array}{r}\mathrm{arcosh}(2x^2-1)=2\mathrm{arch}(x)\text{ ha }x\ge 1\\ \mathrm{arcosh}(8x^4-8x^2+1)=4\mathrm{arch}(x)\text{ ha }x\ge 1\\ \mathrm{arcosh}(2x^2+1)=2\mathrm{arsh}(x)\text{ ha }x\ge 0\\ \mathrm{arcosh}(8x^4+8x^2+1)=4\mathrm{arsh}(x)\text{ ha }x\ge 0\end{array}$

$\mathrm{arsh}u\pm \mathrm{arsh}v=\mathrm{arsh}(u\sqrt{1+v^2}\pm v\sqrt{1+u^2})$

$\mathrm{arch}u\pm \mathrm{arch}v=\mathrm{arch}(uv\pm \sqrt{(u^2-1)(v^2-1)})$

$\begin{array}{rl}\mathrm{arsh}u+\mathrm{arch}v& =\mathrm{arsh}(uv+\sqrt{(1+u^2)(v^2-1)})\\ & =\mathrm{arch}(v\sqrt{1+u^2}+u\sqrt{v^2-1})\end{array}$

$$\begin{gathered} \mathrm{arth}(x)\pm \mathrm{arth}(y)=\mathrm{arth}\left(\frac{x\pm y}{1\pm xy} \\ \right) \end{gathered}$$

$$\begin{gathered} \mathrm{arcth}(x)\pm \mathrm{arcth}(y)=\mathrm{arcth}\left(\frac{1\pm xy}{x\pm y} \\ \right) \end{gathered}$$

$\mathrm{arcsch}2=\ln \mathrm{\Phi }$

ahol $\mathrm{\Phi }$ aranymetszés.

Sorfejtésük

$\mathrm{arsh}x$

$=x-\left(\frac{1}{2}\right)\frac{x^3}{3}+\left(\frac{1\cdot 3}{2\cdot 4}\right)\frac{x^5}{5}-\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)\frac{x^7}{7}+\cdots$

$=\sum _{n=0}^{\mathrm{\infty }}\left(\frac{(-1{)}^n(2n)!}{2^{2n}(n!{)}^2}\right)\frac{x^{2n+1}}{(2n+1)},\left|x\right|<1$

$\mathrm{arch}x$

$=\ln 2x-(\left(\frac{1}{2}\right)\frac{x^{-2}}{2}+\left(\frac{1\cdot 3}{2\cdot 4}\right)\frac{x^{-4}}{4}+\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)\frac{x^{-6}}{6}+\cdots )$

$=\ln 2x-\sum _{n=1}^{\mathrm{\infty }}\left(\frac{(-1{)}^n(2n)!}{2^{2n}(n!{)}^2}\right)\frac{x^{-2n}}{(2n)},x>1$

$\mathrm{arth}x=x+\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{x^{2n+1}}{(2n+1)},\left|x\right|<1$

$\mathrm{arcsch}x=\mathrm{arsh}{x}^{-1}$

$=x^{-1}-\left(\frac{1}{2}\right)\frac{x^{-3}}{3}+\left(\frac{1\cdot 3}{2\cdot 4}\right)\frac{x^{-5}}{5}-\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)\frac{x^{-7}}{7}+\cdots$

$=\sum _{n=0}^{\mathrm{\infty }}\left(\frac{(-1{)}^n(2n)!}{2^{2n}(n!{)}^2}\right)\frac{x^{-(2n+1)}}{(2n+1)},\left|x\right|<1$

$\mathrm{arsch}x=\mathrm{arcosh}{x}^{-1}$

$=\ln \frac{2}{x}-(\left(\frac{1}{2}\right)\frac{x^2}{2}+\left(\frac{1\cdot 3}{2\cdot 4}\right)\frac{x^4}{4}+\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)\frac{x^6}{6}+\cdots )$

$=\ln \frac{2}{x}-\sum _{n=1}^{\mathrm{\infty }}\left(\frac{(-1{)}^n(2n)!}{2^{2n}(n!{)}^2}\right)\frac{x^{2n}}{2n},0<x\le 1$

$\mathrm{arcth}x=\mathrm{artanh}{x}^{-1}$

$=x^{-1}+\frac{x^{-3}}{3}+\frac{x^{-5}}{5}+\frac{x^{-7}}{7}+\cdots$

$=\sum _{n=0}^{\mathrm{\infty }}\frac{x^{-(2n+1)}}{(2n+1)},\left|x\right|>1$

$\mathrm{arsh}x=\ln 2x+\sum _{n=1}^{\mathrm{\infty }}{\left(-1\right)}^{n-1}\frac{\left(2n-1\right)!!}{2n\left(2n\right)!!}\frac{1}{x^{2n}}$

$\begin{array}{rlr}\mathrm{arsh}(x)& =x\sum _{k=0}^{\mathrm{\infty }}\frac{(2k-1)!!(-x^2{)}^k}{(2k)!!(2k+1)}=\sum _{k=0}^{\mathrm{\infty }}\frac{(\genfrac{}{}{0ex}{}{-\frac{1}{2}}{k})x^{2k+1}}{2k+1}& \\ & =x-\frac{1}{2}\frac{x^3}{3}+\frac{1\cdot 3}{2\cdot 4}\frac{x^5}{5}-\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\frac{x^7}{7}+\cdots & \text{ ha }|x|<1\\ \mathrm{arsh}(x)& =\mathrm{sgn}(x)\cdot [\ln (2|x|)-\sum _{k=1}^{\mathrm{\infty }}\frac{(2k-1)!!}{2k(2k)!!(-x^2{)}^k}]& \text{ ha }|x|>1\\ \mathrm{arch}(x)& =\ln (2x)-\sum _{k=1}^{\mathrm{\infty }}\frac{(2k-1)!!}{2k\cdot (2k)!!}{x}^{-2k}& \end{array}$

Deriváltjaik

$\begin{array}{rl}\frac{d}{dx}\mathrm{arsh}x& =\frac{1}{\sqrt{1+x^2}}\\ \frac{d}{dx}\mathrm{arch}x& =\frac{1}{\sqrt{x^2-1}}\\ \frac{d}{dx}\mathrm{arth}x& =\frac{1}{1-x^2}\\ \frac{d}{dx}\mathrm{arcth}x& =\frac{1}{1-x^2}\\ \frac{d}{dx}\mathrm{arsech}x& =\frac{-1}{x(x+1)\sqrt{\frac{1-x}{1+x}}}\\ \frac{d}{dx}\mathrm{arcsch}x& =\frac{-1}{x^2\sqrt{1+\frac{1}{x^2}}}\\ \end{array}$

Valós x értékekre:

$\begin{array}{rl}\frac{d}{dx}\mathrm{arsech}x& =\frac{\mp 1}{x\sqrt{1-x^2}};\mathrm{\Re }\{x\}\gtrless 0\\ \frac{d}{dx}\mathrm{arcsch}x& =\frac{\mp 1}{x\sqrt{1+x^2}};\mathrm{\Re }\{x\}\gtrless 0\end{array}$

Példaként nézzük a következőt: θ = arsh x, így:

$\frac{d\mathrm{arsh}x}{dx}=\frac{d\theta }{d\sinh \theta }=\frac{1}{\cosh \theta }=\frac{1}{\sqrt{1+{\sinh }^2\theta }}=\frac{1}{\sqrt{1+x^2}}$

Határozatlan integrálok

$$\begin{gathered} \int \mathrm{arsh}(x) \\ \mathrm{d}x=x\cdot \mathrm{arsinh}(x)-\sqrt{x^2+1}+C \end{gathered}$$

$$\begin{gathered} \int \mathrm{arch}(x) \\ \mathrm{d}x=x\cdot \mathrm{arcosh}(x)-\sqrt{x^2-1}+C \end{gathered}$$

$\int \mathrm{arth}(x)\mathrm{d}x=x\cdot \mathrm{artanh}(x)+\frac{1}{2}\ln (1-x^2)+C$

$\int \mathrm{arcth}(x)\mathrm{d}x=x\cdot \mathrm{arcoth}(x)+\frac{1}{2}\ln (x^2-1)+C$

$\int \mathrm{arsech}(x)\mathrm{d}x=x\cdot \mathrm{arsech}(x)-\arctan \left(\sqrt{\frac{1}{x^2}-1}\right)+C$

$\int \mathrm{arcsch}(x)\mathrm{d}x=x\cdot \mathrm{arcsch}(x)+\ln (x+x\sqrt{1+x^{-2}})+C.$

Numerikus számítások

Az areasinus hyperbolicus számítható az $\mathrm{arsh}(x)=\ln (x+\sqrt{x^2+1})$ képlettel. Ez azonban nagy, illetve kis abszolútértékű helyeken gondot okoz:

• Nagy értékeknél túlcsordulás jön létre, habár az eredmény nagysága ezt nem indokolja
• Kis értékek esetén vészes kiegyszerűsödés adódik, így az eredmény pontatlan lesz.

A következőkben feltesszük, hogy $x\ge 0$. Ekkor a következő közelítések alkalmazhatók:

• $x$ akkora pozitív szám, hogy $x\ge {10}^{\frac{k}{2}}$:

$\mathrm{arsh}x=\ln 2+\ln x,$

ahol $k$ a szignifikáns számjegyek száma az adott számtípusnál, például double esetén 16.

A képlet a következő meggondolásból adódik:

${10}^k$ a legkisebb pozitív szám, amikor az utolsó számjegy még pontosan elmentődik, így ${10}^k+1\approx {10}^k$ teljesül. Kiszámoljuk azt az $x$-et, amettől kezdve $x^2+1\approx x^2$. Kijön, hogy ez $x^2\ge {10}^k$ esetén van így, ahonnan $x\ge {10}^{\frac{k}{2}}$. Ebben az esetben helyettesíthető $x^2+1$ $x^2$-tel:

$\mathrm{arsh}(x)=\ln (x+\sqrt{x^2+1})$ ≈ $\ln (x+\sqrt{x^2})=\ln (2x)=\ln 2+\ln x$

• $x$ a nullához közeli kis pozitív szám. Ekkor a Taylor-sor alkalmazható. Például, ha $x<0,125$:

$\mathrm{arsinh}x=x-\frac{1}{2}\frac{x^3}{3}+\frac{1\cdot 3}{2\cdot 4}\frac{x^5}{5}-\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\frac{x^7}{7}+\cdots$

• Általános eset: számolhatunk az eredeti képlettel:

$\mathrm{arsh}(x)=\ln (x+\sqrt{x^2+1})$

Az areacosinus hyperbolicus számítható az $\mathrm{arch}(x)=\ln (x+\sqrt{x^2-1})$ képlettel. Ez azonban nagy abszolútértékű helyeken gondot okoz, mivel túlcsordulás jön létre, habár az eredmény nagysága ezt nem indokolja. A kis értékek nem okoznak alulcsordulást, mivel a nulla közelében a függvény nem definiált.

• $x$ akkora pozitív szám, hogy $x\ge {10}^{\frac{k}{2}}$:

$\mathrm{arch}x=\ln 2+\ln x,$

ahol $k$ a szignifikáns számjegyek száma az adott számtípusnál, például double esetén 16.

• $x<1$ esetén a függvény nem definiált.
• Általános esetben, azaz ha $1\le x<{10}^{\frac{k}{2}}$:

$\mathrm{arch}(x)=\ln (x+\sqrt{x^2-1})$

Források

• Pattantyús Gépész- és Villamosmérnökök Kézikönyve 1. kötet. Műszaki Könyvkiadó, Budapest, 1961.
• J. N. Bronstein - K. A. Szemengyajev: Matematikai zsebkönyv. Műszaki könyvkiadó, Budapest, 1987. ISBN 963 1053091
• Christoph Bock: Elemente der Analysis. (PDF; 942 kB) Abschnitt 7.10.
• Eric W. Weisstein: Inverse Hyperbolic Tangent und Inverse Hyperbolic Cotangent auf MathWorld

További információk

• Inverz hiperbolikus függvények a MathWorldben
• PHP programozási segédlet
• Weisstein, Eric W.: Inverse Hyperbolic Sine (angol nyelven). Wolfram MathWorld
• Weisstein, Eric W.: Inverse Hyperbolic Cosine (angol nyelven). Wolfram MathWorld
• Eric W. Weisstein: Inverse Hyperbolic Secant und Inverse Hyperbolic Cosecant auf MathWorld

Fordítás

• Ez a szócikk részben vagy egészben az Areasinus hyperbolicus und Areakosinus hyperbolicus című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
• Ez a szócikk részben vagy egészben az Areatangens hyperbolicus und Areakotangens hyperbolicus című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
• Ez a szócikk részben vagy egészben az Areasekans hyperbolicus und Areakosekans hyperbolicus című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.