Lemniszkáta

A lemniszkáta.

Lemniszkáta szerkesztése. Az ábrán látható háromtagú csuklós mechanizmus középső rúdjának felezőpontja a mechanizmus mozgatása során lemniszkátát ír le.

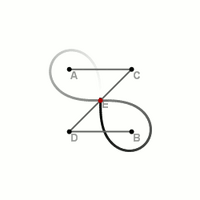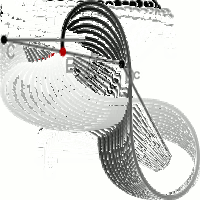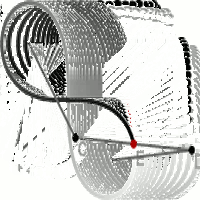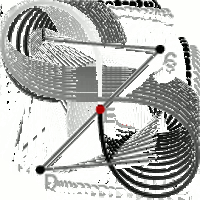
A lemniszkáta egy speciális Cassini-görbe. A Cassini-görbék a sík olyan pontjainak mértani helyei, melyekre igaz, hogy két adott ponttól való távolságának szorzata állandó. Azt a Cassini-görbét nevezzük lemniszkátának, amelyiken rajta van a két adott pontot összekötő szakasz felezőpontja. A lemniszkáta egy 8 (vagy $\mathrm{\infty }$) alakú, negyedrendű síkgörbe.

Egyenletei

Az ábra jelöléseivel derékszögű koordináta-rendszerben:

${(x^2+y^2)}^2-2c^2(x^2-y^2)=0$

Polárkoordinátákkal:

$\rho =c\sqrt{2\cos 2\phi }$

ahol

$\phi \in ⟨-\frac{\pi }{4},\frac{\pi }{4}⟩\cup ⟨\frac{3\pi }{4},\frac{5\pi }{4}⟩$.

Paraméteres egyenletrendszere:

$x=ct\sqrt{2}\frac{1+t^2}{1+t^4}$

$y=ct\sqrt{2}\frac{1-t^2}{1+t^4}$

ahol $t\in \mathbb{ℝ}$.

Tulajdonságai

A görbe polárkoordinátákkal megadott egyenleteihez tartozó görbületi sugár:

$R=\frac{2c^2}{3\rho }=\frac{c\sqrt{1+t^4}}{3|t|}$

feltéve, hogy $\rho \ne 0$, illetve $t\ne 0$. A lemniszkáta egyes hurkainak területe:

$T=c^2$,

Kerülete:

$k\approx 2c\cdot 1,8541$.

Ha az

$x^2-y^2=c^2$

hiperbolát az

$x^2+y^2=c^2$

körön tükrözzük, lemniszkátát kapunk.

Források

• J. N. Bronstein - K. A. Szemengyajev: Matematikai zsebkönyv. Műszaki könyvkiadó, Budapest, 1987. ISBN 963-10-53091
• Pattantyús Gépész- és Villamosmérnökök Kézikönyve 2. kötet. Műszaki Könyvkiadó, Budapest, 1961.