Paralelepipedon

Paralelepipedon
tartalmazó halmaz	hasáb
oldallapok száma	6 (paralelogramma)
élek száma	12
csúcsok száma	8
szimmetria	középpontosan tükrös (centrálszimmetrikus)
konvexitás	konvex

A paralelepipedon olyan hat lap által határolt térbeli geometriai alakzat, amelynek minden oldallapja paralelogramma. A név a görög παραλληλ-επίπεδον (párhuzamos síkok) kifejezésből ered. Három ekvivalens definíció:

• A paralelepipedon egy paralelogramma alapú hasáb.
• A paralelepipedon egy hatoldalú térbeli geometriai alakzat, amelynek minden oldallapja paralelogramma.
• A paralelepipedon egy hatoldalú térbeli geometriai alakzat, amelynek két-két szemközti oldallapja párhuzamos.

A téglatest, a kocka és a romboéder paralelepipedonok. A paralelepipedon egy poliéder.

Tulajdonságok

Bármely párhuzamos oldalpár tekinthető a hasáb alapjának. Négy-négy él párhuzamos és egyenlő hosszúságú. A paralelepipedon előállítható a kocka lineáris leképezéseként. Bármely egybevágó paralelepipedonokkal hézagmentesen kitölthető a tér.

Térfogat

Mivel a paralelepipedon hasáb, térfogata az alaplap területének és az alaplaphoz tartozó magasságnak a szorzata. Magasság alatt az alapsíkok távolságát értjük (az őket összekötő legrövidebb szakasz hossza). A paralelepipedon térfogata kiszámítható az egy csúcsból induló oldalvektorok vegyes szorzataként. $\stackrel{\rightharpoonup }{OA}=\mathbf{a}$
$\stackrel{\rightharpoonup }{OB}=\mathbf{b}$
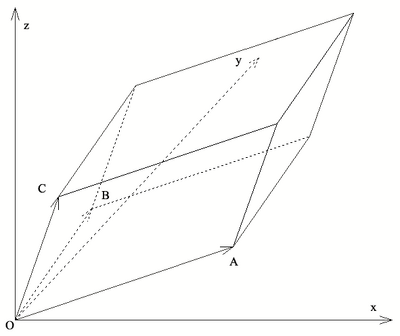
$\stackrel{\rightharpoonup }{OC}=\mathbf{c}$ $V=\mathbf{a}\mathbf{b}\mathbf{c}\equiv (\mathbf{a}\times \mathbf{b})\cdot \mathbf{c}$ Ha a = (a₁, a₂, a₃), b = (b₁, b₂, b₃) és c = (c₁, c₂, c₃), akkor paralelepipedon előjeles térfogata megegyezik az alábbi determináns értékével: $V=\left|\begin{array}{ccc}{a}_1& a_2& a_3\\ b_1& b_2& b_3\\ c_1& c_2& c_3\end{array}\right|$