Szögfelező

A szögfelező szerkesztése körzővel és vonalzóval

A szögfelező a szöget két egyenlő szögre osztja. A szögfelező minden pontja azonos távolságra van a szög száraitól és átmegy a szög csúcsán.

A konvex szögtartományban a két szögszártól azonos távolságra lévő pontok egy félegyenest alkotnak. A szögtartományon kívül e félegyenes meghosszabbítását szoktuk a szögfelezőnek tekinteni, de a félegyenesen kívül is vannak pontok, melyek a szögszáraktól, mint félegyenesektől azonos távolságra vannak. Egyenesek által alkotott szögnél a két egyenestől azonos távolságra lévő pontok két egyenest alkotnak, melyek merőlegesek egymásra.

A szögfelező szerkesztése

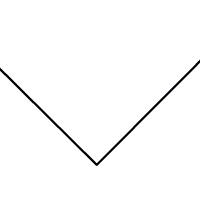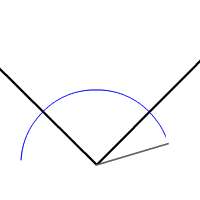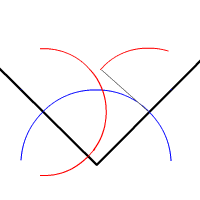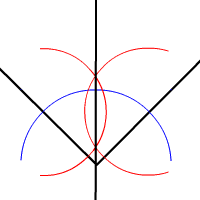
Egy szög szögfelezőjét meg lehet szerkeszteni körzővel és vonalzóval a következő módon: olyan kört rajzolunk, melynek középpontja a szög csúcsa. A körvonal a szög mindkét szárát elmetszi. Rajzoljunk két azonos sugarú kört, melyeknek a középpontja a két metszéspont. A két kör két metszéspontja meghatározza a szöget felező egyenest.

A háromszög szögfelezői

A háromszög belső- (piros) és külső (zöld) szögfelezői, beírt köre (kék) és hozzáírt körei (sárga)

Belső szögfelezők és háromszög beírt köre

A háromszög belső szögfelezői azok az egyenesek, melyek a háromszög belső szögeit elfelezik. Ezeknek az egyeneseknek minden pontja azonos távolságra van a háromszög két-két oldalegyenesétől, mivel szögfelezők. A háromszög belső szögfelezői egy pontban metszik egymást. Ezt beláthatjuk a következőképpen: Az $A$ csúcson és a $B$ csúcson átmenő szögfelezők metszéspontja egyenlő távol van a $b$ és $c$ oldalegyenestől (mivel az $A$ csúcson átmenő szögfelező pontja) valamint a $c$ és $a$ oldalegyenesektől is (mivel a $B$ csúcson átmenő szögfelezőnek is pontja). Tehát mindhárom oldalegyenestől egyenlő távol van, így $a$-tól és $b$-től is, ezért rajta van a $C$-n átmenő szögfelezőn. A belső szögfelezők metszéspontja mindhárom oldaltól azonos távolságra van, ezért ez a pont a háromszög mindhárom oldalát érintő kör középpontja. A kör sugara a középpontból az oldalakra állított merőleges szakasz.

A szögfelezőtétel (Apollóniosz tétele)

Ábra a szögfelezőtétel bizonyításához

A háromszög belső szögfelezője a szemközti oldalt a szomszédos oldalak arányában osztja, vagyis $\frac{x}{y}=\frac{a}{c}$. Bizonyítás: Meghosszabbítjuk a háromszög $c$ oldalát $B$-n túl $a$-val, így kapjuk meg $D$-t. $CBD$ egyenlő szárú háromszög, ennek a $B$ csúcsnál lévő külső szöge $\beta$, az alapon fekvő szögei $\frac{\beta }{2}$ nagyságúak. Az $ABC$ háromszög $c$ oldala és a szögfelező által bezárt szög egyállású a $CBD$ háromszög $D$ csúcsnál levő szögével, mivel a két szög azonos nagyságú és az egyik száruk egy egyenesbe esik. Ezért a szögek másik szára – a szögfelező és a $CD$ oldal – is párhuzamosak egymással. Az $A$ csúcsnál lévő szögre a párhuzamos szelők tételét alkalmazva kapjuk az $\frac{x}{y}=\frac{a}{c}$ egyenlőséget.

Külső szögfelezők és a háromszög hozzáírt körei

A háromszög külső szögeit megfelezve a külső szögfelezőket kapjuk. A szögfelező minden pontja egyenlő távol van a háromszög két oldalegyenesétől. Két-két szögfelező egy pontban metszi egymást. A metszéspont a hozzáírható kör középpontja, mivel mindhárom oldalegyenestől egyenlő távol van. A háromszög egy csúcsból húzott belső és külső szögfelezője merőleges egymásra.

Források

• Kleine Enzyklopädie Mathematik. Leipzig: VEB Verlag Enzyklopädie. 1970. 185, 206, 359. oldal.
• Matematikai kisenciklopédia. Szerk. Lukács Ernőné és Tarján Rezsőné. Budapest: Gondolat. 1968. 210. oldal.