Vonalfelület

A geometriában az a felület vonalfelület, amelynek minden pontján át húzhatunk egy olyan egyenest, ami az adott felületen halad végig. Ilyen például a sík, a hengerpalást vagy a kúpfelület. A vonalfelületet úgy képzelhetjük el, mint egy egyenes térben történő mozgatásának lenyomatát. Pl. kúpfelületet úgy képezhetünk ezzel a módszerrel, hogy egy egyenes egyik pontját rögzítjük, egy másik pontját pedig körbevezetjük egy körön.

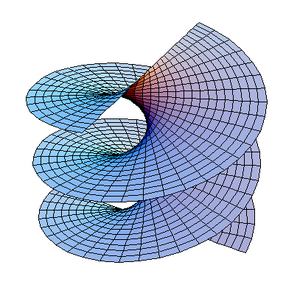
Kétszeres vonalfelület

Kétszeres vonalfelület az a felület, melynek minden pontján át két különböző rajta fekvő egyenes húzható. Ilyen például a sík (ez az egyetlen n-szeres vonalfelület, ha $n\ge 3$), a hiperbolikus paraboloid (nyeregfelület) vagy a hiperbolikus hiperboloid.

Paraméterezés

Csavarfelület

A mozgó egyenes leírható az

$S(t,u)=p(t)+ur(t)$

egyenlettel, ahol $S(t,u)$ a felület általános pontja, $p(t)$ a görbén végigfutó pont, $r(t)$ az egységgömbön, ami végigköveti a görbét. Például, ha

$\begin{array}{rl}p(t)& =(\cos (2t),\sin (2t),0)\\ r(t)& =(\cos t\cos 2t,\cos t\sin 2t,\sin t),\end{array}$

akkor a Möbius-szalag felülete az eredmény. A vonalfelület paraméterezhető úgy is, hogy $S(t,u)=(1-u)p(t)+uq(t)$, ahol $p$ és $q$ a felület két, egymást nem metsző görbéje. Például, ha $p(t)$ és $q(t)$ két kitérő egyenesen fut végig konstans sebességgel, akkor hiperbolikus paraboloidot, vagy egyköpenyű hiperboloidot kapunk.

Síkba teríthető felület

Egy felület síkba teríthető, ha nyújtás vagy összenyomás nélkül síkba teríthető. Ha egy síkba teríthető felület teljes tér a háromdimenziós térben, akkor vonalfelület, így például a gömb nem teríthető síkba. Fordítva viszont nem áll a dolog. A henger- és kúpfelület például síkba teríthető, de az egyköpenyű hiperboloid már nem. Általánosabban, ha a háromdimenziós térben egy felület síkba teríthető, akkor van olyan vonalfelület, ami tartalmazza. Négy dimenzióban viszont léteznek olyan síkba teríthető felületek, amik nem vonalfelületek.

Algebrai geometria

Az z=xy egyenletű hiperbolikus paraboloid

Az algebrai geometriában a vonalfelületeket olyan projektív felületekből származtatják, amik minden pontjára illeszkedik egy egyenes, ami teljes egészében a felület része. Ez a feltétel definícióként is szolgál.

Az építészetben

A kétszeresen vonalazott felületek lehetőséget adnak arra, hogy egyenes építőelemekből görbült felszínt hozzanak létre. Így épülnek hiperbolikus paraboloid alakú nyeregtetők, egyköpenyű hiperboloid alakú hűtőtornyok és szeméttárolók.

• 
  Hiperbolikus hiperboloid alakú hűtőtornyok a Didcot Power Stationnál, Nagy-Britanniában; a felszín kétszeresen vonalazott.
• 
  Kétszeresen vonalfelület alakú víztorony toroid tartállyal. Tervezte Jan Bogusławski, Ciechanów, Lengyelország
• 
  Hiperboloid alakú Kobe Port Torony, Kobe, Japán.
• 
  A moszkvai Suhov-torony kettős vonalfelületének rácsszerkezete.
• 
  Vonalazott csavarfelület alakú csigalépcső (Torrazzo di Cremona).
• 
  Kúp alakú szalmakalap.

Források

• Barth, Wolf P.; Hulek, Klaus; Peters, Chris A.M.; Van de Ven, Antonius (2004), Compact Complex Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge., 4, Springer-Verlag, Berlin, MR2030225, ISBN 978-3-540-00832-3
• Beauville, Arnaud (1996), Complex algebraic surfaces, London Mathematical Society Student Texts, 34 (2nd ed.), Cambridge University Press, MR1406314, ISBN 978-0-521-49510-3; 978-0-521-49842-5
• Edge, W. L. (1931), The Theory of Ruled Surfaces, Cambridge, University Press . Review: Bull. Amer. Math. Soc. 37 (1931), 791-793, doi:10.1090/S0002-9904-1931-05248-4
• Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8 .
• Iskovskikh, V.A. (2001), "Ruled surface", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104