Bode-diagram

Másodfokú aluláteresztő szűrő Bode-diagramja
Fölül az amplitúdó karakterisztika, alul a fázismenet
(kirajzolva MATLABbal)

A Bode-diagram a rendszerelmélet, irányítástechnika, jelfeldolgozás és hálózatszámítás területén elterjedten használt grafikon, mely egy egy bemenetű, egy kimenetű rendszer átviteli karakterisztikájának ábrázolására szolgál. A diagram részét alkotó két részdiagram az átviteli karakterisztika amplitúdóját illetve fázisát ábrázolja a frekvencia függvényében. A diagram nagy előnye más módszerekkel (például Nyquist-diagram) szemben, hogy a frekvenciát és az amplitúdót logaritmikus skálán ábrázolja, így nagy átfogást biztosít. Ez egyben lehetővé teszi, hogy a valós rendszerekben gyakran előforduló, racionális törtfüggvény alakú átviteli karakterisztikák esetén kézzel is viszonylag könnyű közelítő diagramokat rajzolni. A diagram névadója, Hendrik Wade Bode amerikai mérnök az 1930-as években alkalmazta először.

A Bode-diagram felépítése

A Bode-diagramot komplex értékű, egyváltozós függvény, az átviteli karakterisztika ábrázolására használják. Ehhez a komplex szám exponenciális alakját használja fel:

$z=a{e}^{j\phi }$

Ahol az a nemnegatív valós szám z abszolútértéke, a valós φ pedig z árkusza. A komplex értékű H(jω) átviteli karakterisztikát is felírhatjuk

$H(j\omega )=a(\omega )e^{j\phi (\omega )}$

alakban. Bode az a(ω) és a φ(ω) függvényt ábrázolta két diagramon:

• Az amplitúdókarakterisztika az átviteli karakterisztika abszolút értékének frekvenciafüggését mutatja be, a vízszintes tengelyen a frekvenciát, a függőlegesen az amplitúdót ábrázolva.

A körfrekvencia-tengely logaritmikus léptékű, de a lineáris egységben megadott körfrekvencia értékeket kell feltüntetni rajta. A tengelyen két körfrekvencia távolságát, melyek közül az egyik a másik 10-szerese, dekádnak nevezzük, kétszeres frekvenciák távolságát oktávnak. Az amplitúdóskála szintén logaritmikus léptékű, itt azonban a feltüntetett értékek is logaritmikus egységben, decibelben szerepelnek.

$a_{dB}=20{\log }_{10}a$

• A fáziskarakterisztika az átviteli karakterisztika árkuszának (szögének) függvényét tünteti fel. A körfrekvencia-tengely itt is logaritmikus léptékű, a fázisszöget azonban lineáris skálán kell ábrázolni (fokban vagy radiánban kifejezve).

A Bode-diagramban a két részdiagramot egymás fölött helyezik el úgy, hogy a vízszintes (körfrekvencia) tengely a két diagramon fedésben legyen.

A diagram közelítő felrajzolása

Valós pólus vagy zérus hatása

Elsőfokú aluláteresztő karakterisztika számított(Δ) és közelítő értéke

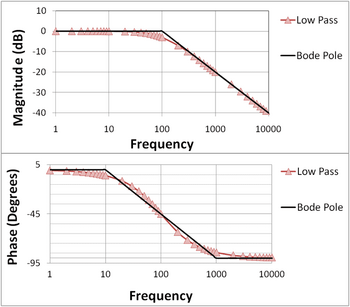
A közelítő (aszimptotikus, töréspontos) ábrázolás abból a meggondolásból indul ki, hogy egy

$H(j\omega )=1+\frac{j\omega }{\mathrm{\Omega }}$

alakú kifejezés (ahol $-\mathrm{\Omega }$ a zérusfrekvencia, $|\mathrm{\Omega }|$ a törésponti körfrekvencia) nagy frekvenciákon $j\omega /\mathrm{\Omega }$-vel, kis frekvenciákon pedig 1-gyel ($0\text{dB}$) közelíthető. Mivel a két közelítő egyenes épp $\omega =\mathrm{\Omega }$-nál metszik egymást, a törtvonalas közelítés amplitúdómenete felrajzolható úgy, hogy kis frekvenciáktól a törésponti frekvenciáig 0 dB-nél halad, majd innentől $j\omega /\mathrm{\Omega }$ abszolút értékének megfelelő egyenessel, 20 dB/dekáddal emelkedik. A fázis közelítésénél jól látható, hogy kis frekvenciáknál 0-val, nagy frekvenciáknál 90°-kal (pozitív $\mathrm{\Omega }$) vagy -90°-kal (negatív $\mathrm{\Omega }$) számolhatunk. A törésponti érték pedig $|1+j|=\sqrt{2}=+3dB$. Az átmeneti tartományt a törésponti frekvencia tizede és tízszerese között szokták meghatározni, az említett határoknál már 0° illetve 90° közelítést alkalmazva. Ez mindössze

$arctg(0,1)\approx 5,71^{\circ }$

hibát okoz. Pólust tartalmazó tag esetén hasonló a helyzet, ekkor a

$H(\omega )=\frac{1}{1+\frac{j\omega }{\mathrm{\Omega }}}$

alakú, egypólusú rendszer átviteli karakterisztikája az előbb tárgyalténak a reciproka. Ezért az amplitúdómenet az előbbi reciproka lesz, vagyis a törésponti frekvencia után -20 dB/dekáddal csökkenő egyenest kell rajzolni. A fázismenetben a reciprok képzés miatt a fázis a -1-szeresére változik, előjelet vált. Megjegyzendő, hogy stabil rendszerekben nem lehet pozitív a pólusfrekvencia, ezért stabil rendszereknél $\mathrm{\Omega }$ mindig pozitív.

Konjugált zérus- illetve póluspárok

Egy nevezőjében másodfokú, számlálójában nulladfokú átviteli karakterisztika általános alakja

$H_2(j\omega )=\frac{1}{1+2\zeta \frac{j\omega }{\mathrm{\Omega }}+{\left(\frac{j\omega }{\mathrm{\Omega }}\right)}^2}$

ahol $\mathrm{\Omega }$ a másodfokú pólusfrekvencia, $\zeta$ (zeta) a csillapítási tényező (a jósági tényező reciproka). $\zeta >=1$ esetén a függvénynek két valós pólusa van, $\zeta <1$ esetén két konjugált komplex pólusa. A karakterisztika abszolút értéke és fázisa

${\log }_{10}|H_2(j\omega )|={\log }_{10}[{(1-{\left(\frac{\omega }{\mathrm{\Omega }}\right)}^2)}^2+{\left(2\zeta \frac{\omega }{\mathrm{\Omega }}\right)}^2]$

illetve

${\phi }_2(\omega )=-arctg\frac{2\zeta \frac{\omega }{\mathrm{\Omega }}}{1-{\left(\frac{\omega }{\mathrm{\Omega }}\right)}^2}$

Az átviteli karakterisztika közelítő értéke $\mathrm{\Omega }>0$ esetén

	$0<\omega <<\mathrm{\Omega }$	$\omega =\mathrm{\Omega }$	$\mathrm{\Omega }<<\omega$
$H_2(j\omega )$	$1$	$1/j2\zeta$	$-{\left(\frac{\mathrm{\Omega }}{\omega }\right)}^2$
$20{\log }_{10}|H_2(j\omega )|$	$0\text{dB}$	$-20lg\left(\frac{1}{2\zeta }\right)\text{dB}$	$-40lg\left(\frac{\omega }{\mathrm{\Omega }}\right)\text{dB}$
${\phi }_2(\omega )$	$0\text{°}$	$-90\text{°}$	$-180\text{°}$

Vagyis törtvonalas közelítés esetén kis frekvenciákon az amplitúdókarakterisztikát a 0 dB-s aszimptotájával, a fáziskarakterisztikát a 0°-os aszimptotával közelíthetjük, nagy frekvencián az $(\mathrm{\Omega },0dB)$ ponton átmenő, -40 dB/dekád meredekségű egyenessel illetve -180°-kal becsülhető a karakterisztika. A fázis átmeneti tartománya ${\omega }_1=10^{-\zeta }\mathrm{\Omega }$ és ${\omega }_2=10^{\zeta }\mathrm{\Omega }$ között egy $({\omega }_1,0\text{°})$, $({\omega }_2,-180\text{°})$ pontokon áthaladó egyenessel közelíthető. Mint a táblázat is mutatja, az átmeneti tartományban a másodfokú átviteli karakterisztika amplitúdója a csillapítási tényező függvényében nagymértékben eltérhet az aszimptotától. Másodfokú számlálóval rendelkező átviteli karakterisztika fáziskarakterisztikája valamint amplitúdókarakterisztikája decibelben a fent vázolt karakterisztikák mínusz egyszerese.

Többtényezős átviteli karakterisztika eredője

Általános esetben az átviteli karakterisztika

$H(\omega )=\prod _{i=0}^{n-1}{H}_i(\omega )$

alakban írható fel. A logaritmus azonosságok miatt

${\log }_{10}|H(\omega )|=\sum _{i=0}^{n-1}{\log }_{10}|H_i(\omega )|$

Ezen kívül $\arg \{H(\omega )\}=\sum _{i=0}^{n-1}\arg \{H_i(\omega )\}$ Vagyis az n tényező szorzataként előálló átviteli karakterisztika mind az amplitúdó- mind a fáziskarakterisztikája a tényezők karakterisztikájának összege.

Diszkrét idejű rendszerek

A diszkrét idejű rendszerek átviteli karakterisztikáját tipikusan nem az eredeti Bode-diagramon ábrázolják, de hasonló diagramokat használnak ezen a területen is. Az amplitúdókarakterisztikát és a fáziskarakterisztikát lineáris frekvenciatengellyel ábrázolják, további különbség, hogy az amplitúdót az esetek egy részében szintén lineáris egységben tüntetik fel. Mivel e rendszerek átviteli karakterisztikája általában $e^{j\omega T_S}$-ben (T_S a mintavételi periódusidő) és nem $j\omega T_S$-ben racionális törtfüggvény, az átviteli karakterisztika $e^{j\omega T_S}$ periodikus jellegéből következően ω_S=2π/T_S többszöröseivel eltolva ismétlődik. Elég tehát csak az ω∈[0, ω_S] intervallumon ábrázolni. A Bode-diagram egyik fő előnyére, a nagy átfogásra itt nincs szükség, mert mintavételezett rendszerekben mivel a mintavételi frekvenciát a számítási igény csökkentése érdekében célszerű minimális szinten tartani, így a rendszerek körfrekvencia-tartománya viszonylag jól kitölti a [0, ω_S] intervallumot, a lineáris felbontás itt megfelelő. Emellett egyszerű felrajzolásának előnye is elveszik ebben a környezetben épp amiatt, mert az átviteli karakterisztika nem $j\omega T_S$ racionális törtfüggvénye. Lineáris körfrekvencia-tengely és logaritmikus amplitúdótengely esetén lenne lehetőség a fentebb vázolt tört vonalas közelítés alkalmazására. Egyéb praktikus megfontolások is ebbe az irányba mutatnak. Egy rendszer analíziséhez gyakran használják a diszkrét Fourier-transzformációt, aminek a frekvenciabeli felbontása lineáris léptékben állandó, ω_S/N (N a felhasznált minták száma).

Források

Fodor György. Hálózatok és rendszerek. Műegyetem Kiadó (2004). ISBN 963 420 810 X