Háromszög-egyenlőtlenség

A háromszög-egyenlőtlenség a geometria egyik legalapvetőbb tétele, megállapítható segítségével, hogy három szakaszból lehet-e háromszöget szerkeszteni. Az egyenlőtlenség tovább általánosítható valós és komplex számokra, összegzésekre, integrálokra és különböző terekre. Itt a hosszak szerepét abszolútértékek és különféle normák veszik át. Leginkább becslésekben használják a matematika több területén is.

A tétel

Egy háromszögben két oldal hosszának az összege nagyobb, mint a harmadik oldal hossza. Azaz: $a<b+c$ és $b<a+c$ és $c<a+b$. A tétel ekvivalens alakja: $a-b<c$, $b-c<a$ és $c-a<b$ Bizonyítás: $AC+CB>AB$ -t elég bizonyítani. Hosszabbítsuk meg az $AC$ oldalt, és felmérjük a $CB$ távolságot a meghosszabbított félegyenesre, így kapjuk a $CD$ szakaszt. $BCD$ háromszög egyenlő szárú, ekkor $CBD$ szög = $CDB$ szög. $BC$ az $ABD$ szög belsejében halad, ekkor $ABD$ szög > $CBD$ szög = $CDB$ szög, így $AD>AB$. Ez viszont éppen a tételben szereplő $a+b>c$.

Metrikus interpretáció

A háromszög-egyenlőtlenség biztosítja, hogy a kétdimenziós (általánosabban, az n dimenziós) euklideszi tér tetszőleges három A,B,C pontjára igaz legyen, hogy bármely kettő pár egymástól mért távolságainak összege nagyobb, mint a harmadik pár közt mért távolsága:

AB+BC≥AC BC+CA≥BA CA+AB≥BC

Ezt a tényt úgy is interpretálhatjuk, hogy "két pont között a legrövidebb út az egyenes", mert a háromszög-egyenlőtlenség egy speciális esete e kijelentésnek, míg utóbbi következménye az előbbinek. A háromszög-egyenlőtlenség e változata megenged elfajult háromszögeket, amikor is néhány háromszögcsúcs vagy -oldal illeszkedik egymásra.

A tétel általánosításai

Valós számokra

Valós számokra: $|a+b|\le |a|+|b|=||x|-|a||\le |x-a|.$ Bizonyítás: Mivel az egyenlőtlenség mindkét oldala nem negatív, ezért a négyzetre emelés ekvivalens átalakítás:

$$\begin{gathered} a^2+2ab+b^2 \\ \le \\ {a}^2+2|ab|+b^2. \end{gathered}$$

Mindkét oldalból kivonva az azonos tagokat:

$2ab\le 2|ab|.$

és ez mindig teljesül, mert $x\le |x|$ minden $x\in \mathbb{ℝ}.$-re. Valós számokra önállóan is belátható a háromszög-egyenlőtlenség kivonásos alakja: Nyilván $|a+b|-|b|\le |a|.$ Az

$a:=x+y,b:=-y$

helyettesítéssel

$|x|-|y|\le |x+y|.$

Viszont, ha

$b:=-x$

akkor

$|y|-|x|\le |x+y|,$

Az előző két egyenlőtlenséget összetéve

$||x|-|y||\le |x+y|\le |x|+|y|.$

y helyére -y-t téve

$||x|-|y||\le |x-y|\le |x|+|y|.$

Összefoglalva

$||x|-|y||\le |x\pm y|\le |x|+|y|$ minden $x,y\in \mathbb{ℝ}$-re.

Komplex számokra

Komplex számokra a háromszög-egyenlőtlenség:

$|z_1+z_2|\le |z_1|+|z_2|.$

Bizonyítás: Mivel egyik oldal sem lehet negatív, ezért a négyzetre emelés ekvivalens átalakítás:

$z_1\overline{z_1}+z_1\overline{z_2}+\underset{=\overline{z_1\stackrel{‾}{z_2}}}{\underbrace{\overline{z_1}{z}_2}}+z_2\overline{z_2}\le z_1\overline{z_1}+2\underset{=|z_1\overline{z_2}|}{\underbrace{|z_1{z}_2|}}+z_2\overline{z_2},$

ahol a felülvonás a komplex konjugálást jelenti. A két oldalról eltávolítva az egyenlő tagokat, és a $z:=z_1\overline{z_2}$ helyettesítést elvégezve

$z+\overline{z}\le 2|z|$

A z komplex szám algebrai alakja legyen $z=u+iv$. Ezzel

$(u+iv)+(u-iv)=2u\le 2\sqrt{u^2+v^2}$

és

$|u|\le \sqrt{u^2+v^2},$

ami $0\le v^2$ és a valós négyzetgyökfüggvény monotóniája miatt mindig fennáll. A valós esethez hasonlóan látható be a kivonásos alak is

$||z_1|-|z_2||\le |z_1\pm z_2|\le |z_1|+|z_2|$ minden $z_1,z_2\in \mathbb{ℂ}$-re.

Összegekre és integrálokra

A háromszög-egyenlőtlenség többszöri alkalmazásával és teljes indukcióval

$\left|\sum _{i=1}^n{x}_i\right|\le \sum _{i=1}^n\left|x_i\right|$

ahol az $x_i$ számok lehetnek valósak, vagy komplexek. Integrálokra: Legyen az $f:I\to \mathbb{ℝ}$ függvény Riemann-integrálható, ahol $I=[a,b]$ egy intervallum! Ekkor

$|\underset{I}{\int }f(x)dx|\le \underset{I}{\int }|f(x)|dx$.

Hasonlók teljesülnek komplex értékű függvényekre is: $f:I\to \mathbb{ℂ}$. Ekkor ugyanis van egy komplex $\alpha$ úgy, hogy $\alpha \underset{I}{\int }f(x)dx=\left|\underset{I}{\int }fdx\right|$ és $|\alpha |=1$. Mivel

$|\underset{I}{\int }f(x)dx|=\alpha \underset{I}{\int }f(x)dx=\underset{I}{\int }\alpha f(x)dx=\underset{I}{\int }\mathrm{Re}(\alpha f(x))dx+i\underset{I}{\int }\mathrm{Im}(\alpha f(x))dx$

valós, ezért $\underset{I}{\int }\mathrm{Im}(\alpha f(x))dx$ szükségképpen egyenlő nullával. Emellett

$\mathrm{Re}(\alpha f(x))\le |\alpha f(x)|=|f(x)|$,

összetéve tehát

$|\underset{I}{\int }f(x)dx|=\underset{I}{\int }\mathrm{Re}(\alpha f(x))dx\le \underset{I}{\int }|f(x)|dx$.

Vektorokra

Vektorokra:

$|\overrightarrow{a}+\overrightarrow{b}|\le \left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|$.

Négyzetre emeléssel:

${|\overrightarrow{a}+\overrightarrow{b}|}^2=⟨\overrightarrow{a}+\overrightarrow{b},\overrightarrow{a}+\overrightarrow{b}⟩={\left|\overrightarrow{a}\right|}^2+2⟨\overrightarrow{a},\overrightarrow{b}⟩+{\left|\overrightarrow{b}\right|}^2\le {\left|\overrightarrow{a}\right|}^2+2\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|+{\left|\overrightarrow{b}\right|}^2={(\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|)}^2$,

és a Cauchy–Schwarz–Bunyakovszkij-egyenlőtlenség felhasználásával:

$⟨\overrightarrow{a},\overrightarrow{b}⟩\le \left|\overrightarrow{a}\right|\cdot \left|\overrightarrow{b}\right|$.

Innen, mint a valós esetben:

$|\left|\overrightarrow{a}\right|-\left|\overrightarrow{b}\right||\le |\overrightarrow{a}\pm \overrightarrow{b}|\le \left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|$

és

$\left|\sum _{i=1}^n\overrightarrow{a_i}\right|\le \sum _{i=1}^n\left|\overrightarrow{a_i}\right|.$

Gömbháromszögekre

Két általános gömbháromszög

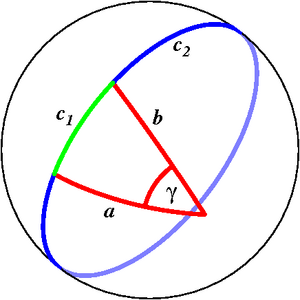
A gömbháromszögek körében a háromszög-egyenlőtlenség azokra a háromszögekre korlátozódik, amiknek egyik oldala sem nagyobb egy fél főkörívnél, azaz a < π, b < π és c < π. Általános gömbháromszögekre a tétel nem igaz. Ahogy az ábra mutatja:

$|a-b|\le c_1\le a+b,$

de $c_2>a+b$, ahol még az is igaz, hogy $c_2>\pi .$

Normált terekben

Az $(X,\Vert .\Vert )$ normált térben a háromszög-egyenlőtlenség ezt az alakot ölti:

$\Vert x+y\Vert \le \Vert x\Vert +\Vert y\Vert$

és megkövetelik, hogy a tér az adott normával ezt az egyenlőtlenséget azonossággal teljesítse. Ebből

$|\Vert x\Vert -\Vert y\Vert |\le \Vert x\pm y\Vert \le \Vert x\Vert +\Vert y\Vert$

és

$\Vert \sum _{i=1}^n{x}_i\Vert \le \sum _{i=1}^n\Vert x_i\Vert$ minden $x_i\in X$-re.

Speciálisan, az L^p-terekben a háromszög-egyenlőtlenséget Minkowski-egyenlőtlenségnek nevezik, és a Hölder-egyenlőtlenséggel bizonyítják.

Metrikus terekben

Az $(X,d)$ metrikus térben a háromszög-egyenlőtlenség ezt az alakot ölti: $d(x,y)\le d(x,z)+d(z,y)$ és megkövetelik, hogy a tér az adott d távolságfüggvénnyel ezt az egyenlőtlenséget azonossággal teljesítse. Innen következik $|d(x,z)-d(z,y)|\le d(x,y)$ és $d(x_0,x_n)\le \sum _{i=1}^{n}d(x_{i-1},x_i)$ a tér tetszőleges elemeire.

Források

• Obádovics J. Gyula: Matematika