Khí-eloszlás

A valószínűségszámítás elméletében, és a statisztika területén a khí-eloszlás egy folytonos valószínűség eloszlás. A khí-eloszlás standard normális eloszlású, független, véletlenszerű változók négyzetei összegének a négyzetgyöke. A legismertebb példa a khí-eloszlásra, a normalizált molekuláris sebességek Maxwell eloszlása, 3 szabadságfokkal (egy szabadságfok , minden térbeli koordinátára). Ha $X_i$ k független, normális eloszlású véletlenszerű változók, ${\mu }_i$ középértékkel, és ${\sigma }_i$ szórással, akkor a statisztika

$Y=\sqrt{\sum _{i=1}^k{\left(\frac{X_i-{\mu }_i}{{\sigma }_i}\right)}^2}$

khí-eloszlású lesz. A khí-eloszlásnak a $k$ paramétere a szabadságfokok számát határozza meg (azaz a $X_i$ számát).

Jellemzők

Khí valószínűségsűrűség-függvény

Kumulatív eloszlásfüggvény

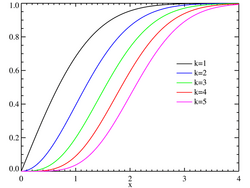
Valószínűségsűrűség-függvény

A valószínűségsűrűség-függvény:

$f(x;k)=\frac{2^{1-\frac{k}{2}}{x}^{k-1}{e}^{-\frac{x^2}{2}}}{\mathrm{\Gamma }(\frac{k}{2})}$

ahol $\mathrm{\Gamma }(z)$ a gamma-függvény.

Kumulatív eloszlásfüggvény

A kumulatív eloszlásfüggvény:

$F(x;k)=P(k/2,x^2/2)$

ahol $P(k,x)$ a szabályozott gamma-függvény.

Függvénygenerálás

Momentum-generáló függvény

A momentum-generáló függvény:

$M(t)=M(\frac{k}{2},\frac{1}{2},\frac{t^2}{2})+$

$t\sqrt{2}\frac{\mathrm{\Gamma }((k+1)/2)}{\mathrm{\Gamma }(k/2)}M(\frac{k+1}{2},\frac{3}{2},\frac{t^2}{2})$

Karakterisztikus függvény

A karakterisztikus függvény:

$\phi (t;k)=M(\frac{k}{2},\frac{1}{2},\frac{-t^2}{2})+$

$it\sqrt{2}\frac{\mathrm{\Gamma }((k+1)/2)}{\mathrm{\Gamma }(k/2)}M(\frac{k+1}{2},\frac{3}{2},\frac{-t^2}{2})$

ahol $M(a,b,z)$ Kummer hipergeometrikus függvénye.

Tulajdonságok

Momentumok

A nyers momentumok:

${\mu }_j=2^{j/2}\frac{\mathrm{\Gamma }((k+j)/2)}{\mathrm{\Gamma }(k/2)}$

ahol $\mathrm{\Gamma }(z)$ a Gamma-függvény. Az első nyers momentumok:

${\mu }_1=\sqrt{2}\frac{\mathrm{\Gamma }((k+1)/2)}{\mathrm{\Gamma }(k/2)}$

${\mu }_2=k$

${\mu }_3=2\sqrt{2}\frac{\mathrm{\Gamma }((k+3)/2)}{\mathrm{\Gamma }(k/2)}=(k+1){\mu }_1$

${\mu }_4=(k)(k+2)$

${\mu }_5=4\sqrt{2}\frac{\mathrm{\Gamma }((k+5)/2)}{\mathrm{\Gamma }(k/2)}=(k+1)(k+3){\mu }_1$

${\mu }_6=(k)(k+2)(k+4)$

ahol a jobb oldali kifejezések származtatása a gamma-függvényből ered:

$\mathrm{\Gamma }(x+1)=x\mathrm{\Gamma }(x)$

Ezekből a kifejezésekből a következő összefüggéseket származtathatjuk: Középérték: $\mu =\sqrt{2}\frac{\mathrm{\Gamma }((k+1)/2)}{\mathrm{\Gamma }(k/2)}$ Szórásnégyzet: ${\sigma }^2=k-{\mu }^2$ Torzulás: ${\gamma }_1=\frac{\mu }{{\sigma }^3}(1-2{\sigma }^2)$ Többlet lapultság: ${\gamma }_2=\frac{2}{{\sigma }^2}(1-\mu \sigma {\gamma }_1-{\sigma }^2)$

Entrópia

Az entrópia:

$S=\ln (\mathrm{\Gamma }(k/2))+\frac{1}{2}(k-\ln (2)-(k-1){\psi }_0(k/2))$

ahol ${\psi }_0(z)$ a poligamma-függvény.

Kapcsolódó eloszlások

• Ha $X\sim {\chi }_k(x)$ akkor $X^2\sim {\chi }_k^2$ (Khí-négyzet eloszlás)
• $$\begin{gathered} \underset{k\to \mathrm{\infty }}{\lim }\frac{{\chi }_k(x)-{\mu }_k}{{\sigma }_k}\stackrel{d}{\to } \\ N(0,1) \end{gathered}$$ (normális eloszlás)
• If $X\sim {\chi }_1(x)$ then $\sigma X\sim HN(\sigma )$ (fél-normális eloszlás) for any $\sigma >0$
• ${\chi }_2(x)\sim \mathrm{R}\mathrm{a}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}(1)$ (Rayleigh-eloszlás)
• ${\chi }_3(x)\sim \mathrm{M}\mathrm{a}\mathrm{x}\mathrm{w}\mathrm{e}\mathrm{l}\mathrm{l}(1)$ (Maxwell-eloszlás)
• $\Vert {\mathit{N}}_{i=1,\dots ,k}(0,1)\Vert \sim {\chi }_k(x)$ (Az n standard normális eloszlás változói normája, a khí-eloszlás k szabadságfokkal.
• a khí-eloszlás az általánosított gamma-eloszlás speciális esete.

Különböző khí and khí-négyzet eloszlások

Név	Statisztika
Khí-négyzet eloszlás	$\sum _{i=1}^k{\left(\frac{X_i-{\mu }_i}{{\sigma }_i}\right)}^2$
nem centrális khí-négyzet eloszlás	$\sum _{i=1}^k{\left(\frac{X_i}{{\sigma }_i}\right)}^2$
khí-eloszlás	$\sqrt{\sum _{i=1}^k{\left(\frac{X_i-{\mu }_i}{{\sigma }_i}\right)}^2}$
nem centrális khí-eloszlás	$\sqrt{\sum _{i=1}^k{\left(\frac{X_i}{{\sigma }_i}\right)}^2}$

Kapcsolódó szócikkek

• Statisztika
• Nakagami-eloszlás
• Norma
• Rayleigh-eloszlás
• Matematikai statisztika
• Khí-négyzet eloszlás
• Normális eloszlás
• Szórás
• Gamma-eloszlás