Koszinusztétel

Jelölések

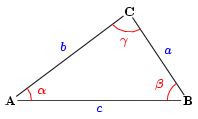
A koszinusztétel a derékszögű háromszögekre vonatkozó Pitagorasz-tétel általánosítása tetszőleges háromszögekre. Az ábra jelöléseivel:

$c^2=a^2+b^2-2ab\cos \gamma$

vagy másként:

$\cos \gamma =\frac{a^2+b^2-c^2}{2ab}$

Bizonyítások

Háromszögekre bontással

A tétel bizonyítható egy háromszög két derékszögű háromszögre való felbontásával.

Koszinusztétel bizonyítása

Ekkor az ábrán bal oldalon látható derékszögű háromszögre felírva a Pitagorasz-tételt kapjuk az állítást:

$c^2$	$=(b-a\cos (\gamma ){)}^2+(a\sin (\gamma ){)}^2$
	$=b^2-2ab\cos (\gamma )+a^2({\cos }^{}(\gamma )+{\sin }^{}(\gamma ))$
	$=a^2+b^2-2ab\cos (\gamma ),$

felhasználva a ${\cos }^2(\gamma )+{\sin }^2(\gamma )=1$ trigonometriai azonosságot. QED

Megjegyzés

Ez a bizonyítás egy kisebb módosítást igényel, ha $b<a\cos (\gamma )$. Ebben az esetben a bal oldali háromszög, amire felírtuk a Pitagorasz-tételt, a háromszögön kívül lesz. A változás a bizonyításban csupán az, hogy $b-a\cos (\gamma )$ helyett $a\cos (\gamma )-b$ szerepel. Mivel a bizonyításban ennek a mennyiségnek csak a négyzete szerepel, a bizonyítás maradék része változatlan marad.

Vektorok segítségével

Az $ABC$ háromszög adott. $C$-ből indítsuk a helyvektorokat. $A$-ba mutató vektor legyen $a$. $B$-be mutató vektor legyen $b$. Az $a$ és $b$ vektorok hajlásszöge legyen $\gamma$. Ekkor $c=a-b$ ⇒ $c^2=(a-b{)}^2$ ⇔ $|c{|}^2=|a{|}^2+|b{|}^2-2|a||b|\cos \gamma$. (Mert a skaláris szorzat disztributív a vektorösszeadásra nézve.) QED

Koordinátarendszerben

Koszinusztétel bizonyítása koordináta-rendszerben

Helyezzük el az $ABC\mathrm{△}$-et derékszögű koordináta-rendszerben úgy, hogy a $C$ csúcs az origóba essen, és a $B$ csúcs az x tengelyre kerüljön. A háromszögben legyen adott $CA=b,CB=a$ oldal és a $BCA\mathrm{\angle }=\gamma$ szög, így a $B$ csúcs koordinátái $B(b,0)$. Ekkor az $A$ csúcs koordinátái $A(b\cos \gamma ;b\sin \gamma )$. Az $AB=c$ oldal hosszúságára a Pitagorasz-tétel alkalmazásával kapjuk:

$\begin{array}{rl}{c}^2& ={(b-a\cos \gamma )}^2+{(0-a\sin \gamma )}^2\\ c^2& =b^2+a^2{\cos }^2\gamma -2ab\cos \gamma +a{\sin }^{}\gamma \\ c^2& =b^2+a^2\underset{=1}{\underbrace{({\cos }^2\gamma +{\sin }^2\gamma )}}-2ab\cos \gamma \\ c^2& =a^2+b^2-2ab\cos \gamma \end{array}$

QED

Megjegyzés

A bizonyítás során nem kellett figyelembe venni a két oldal által bezárt szög típusát, ezért bármilyen háromszögre általánosan igaz. Emellett minimalista abban a tekintetben, hogy a lehető legkevesebb előfeltétellel él (pont koordinátái, Pitagorasz tétele).

Alkalmazások

A koszinusztétel segítségével meg lehet határozni egy háromszög többi adatát két oldalából és az általuk közbezárt szögből vagy három oldalból. Az utóbbi esetben célszerű a meghatározást a legnagyobb oldallal szemközti szöggel kezdeni, így ugyanis a többi szög a szinusztétel használatával is egyértelmű lesz (mivel ezek már biztosan hegyesszögek).

Források

• Weisstein, Eric W.: Koszinusztétel (angol nyelven). Wolfram MathWorld

Kapcsolódó szócikkek

• Tangenstétel
• Szinusztétel
• Kotangenstétel
• Vetületi tétel
• Trigonometrikus azonosságok
• Mollweide-formula