Nemlineáris optika

A nemlineáris optika (NLO) az optika azon területe, ami a fény viselkedését írja le nemlineáris közegben, azaz olyan közegben, amiben a polarizáció nemlineárisan függ a fény elektromos mezejétől. Ez a nemlineárisság általában nagy fényintenzitás esetén figyelhető meg, tipikusan lézer impulzusoknál.

A nemlineáris optika alapjai

Az anyagok elektromos és mágneses tulajdonságait az $\overrightarrow{E}-\overrightarrow{D}$ és $\overrightarrow{B}-\overrightarrow{H}$ vektorok közötti kapcsolatok írják le. Ezen kapcsolatok rendkívül változatos módon függnek az anyagi minőségtől. A legtöbb anyag csak akkor mutat elektromos és mágneses tulajdonságokat, ha azt külső mezőbe helyezzük. Kivételt képeznek ez alól a ferroelektromos és ferromágneses anyagok. Az anyagok nagy részénél a dipólusmomentum sűrűség nulla, mivel a ${\overrightarrow{p}}_n$ atomi dipólusmomentumok minden irányba egyforma súllyal mutatnak, így $\sum _n{\overrightarrow{p}}_n=\overrightarrow{0}$. Ha viszont az anyagot külső mezőbe helyezzük, a közeg dipólusait saját irányába igyekszik befordítani. Az így keletkező polarizáció az anyag belsejében izotróp esetben arányos az adott helyen fellépő elektromos térerősséggel:

$\overrightarrow{P}={ϵ}_0\chi \overrightarrow{E}$

ahol ${ϵ}_0$ a vákuum permittivitása, $\chi$ neve pedig elektromos szuszceptibilitás. A fenti esetben mindkettő skalármennyiség. Anizotróp esetben $\chi$ leírása egy 3x3-as tenzorral történik, így a polarizáció- és térerősségvektor kapcsolatát magasabb rendű közelítések esetén egy-egy alkalmasan választott tenzor írja le:

$\overrightarrow{P}={ϵ}_0\cdot ({\chi }^{(1)}+{\chi }^{(2)}\overrightarrow{E}+{\chi }^{(3)}{\overrightarrow{E}}^2+...)\overrightarrow{E}$

ahol ${\chi }^{(1)}=n^2-1$ a lineáris szuszceptibilitás tenzor, ${\chi }^{(2)},{\chi }^{(3)},...$ pedig a másod-, harmad- stb. rendű szuszceptibilitás tenzorok (ezek matematikai rendje eggyel nagyobb az elnevezésben szereplő számnál). A fenti összefüggést röviden a $\overrightarrow{P}={\overrightarrow{P}}_L+{\overrightarrow{P}}_{NL}$ alakban írhatjuk fel. ${\overrightarrow{P}}_L$ a lineáris, ${\overrightarrow{P}}_{NL}$ pedig a nemlineáris polarizációvektor. Nagy térerősség esetén minden anyag nemlineáris tulajdonságokat mutat.

Nemlineáris hullámegyenlet

Induljunk ki a Maxwell-egyenletek alábbi alakjából, ahol nincsenek jelen töltések (ρ = 0), valamint nem folyik áram (j = 0): M1: $\mathrm{\nabla }\times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$ M2: $\mathrm{\nabla }\overrightarrow{E}=0$ M3: $\mathrm{\nabla }\times \overrightarrow{H}=\frac{\partial \overrightarrow{D}}{\partial t}$ M4: $\mathrm{\nabla }\overrightarrow{B}=0$ A fentiekben $\overrightarrow{B}=\mu \overrightarrow{H}$, illetve $\overrightarrow{D}={ϵ}_0\overrightarrow{E}+{\overrightarrow{P}}_L+{\overrightarrow{P}}_{NL}={ϵ}_0\cdot (1+\chi )\overrightarrow{E}+{\overrightarrow{P}}_{NL}=ϵ\overrightarrow{E}+{\overrightarrow{P}}_{NL}$. M3-at idő szerint deriválva, illetve véve M1 rotációját, a következő összefüggésre jutunk: (1): $\mathrm{\nabla }\times \frac{\partial \overrightarrow{H}}{\partial t}=ϵ\frac{{\partial }^2\overrightarrow{E}}{\partial t^2}+\frac{{\partial }^2{\overrightarrow{P}}_{NL}}{\partial t^2}$ (2): $\mathrm{\nabla }\times \mathrm{\nabla }\times \overrightarrow{E}=-\mu \mathrm{\nabla }\times \frac{\partial \overrightarrow{H}}{\partial t}$ Az utóbbi egyenlet és M2 felhasználásával a (3): $\mathrm{\nabla }\times \mathrm{\nabla }\times \overrightarrow{E}=\mathrm{\nabla }(\mathrm{\nabla }\overrightarrow{E})-\mathrm{\Delta }\overrightarrow{E}=-\mathrm{\Delta }\overrightarrow{E}$ összefüggést kapjuk. Ezek után (1)-et (2)-be írva, felhasználva a (3)-as összefüggést, az alábbi differenciálegyenlet adódik: $\mathrm{\Delta }\overrightarrow{E}-\mu ϵ\frac{{\partial }^2\overrightarrow{E}}{\partial t^2}=\mu \frac{{\partial }^2{\overrightarrow{P}}_{NL}}{\partial t^2}$ Felhasználva az $n=\sqrt{{ϵ}_r{\mu }_r}$ és $c=\frac{1}{\sqrt{{\mu }_0{ϵ}_0}}$ összefüggéseket, az alábbi differenciálegyenlet áll elő:

$\mathrm{\Delta }\overrightarrow{E}-\frac{n^2}{c^2}\frac{{\partial }^2\overrightarrow{E}}{\partial t^2}=\mu \frac{{\partial }^2{\overrightarrow{P}}_{NL}}{\partial t^2}.$

A fenti egyenletet nemlineáris hullámegyenletnek nevezzük, azaz a fenti differenciálegyenlet írja le a fény nemlineáris optikai viselkedését. Az anyagok döntő többségében igaz, hogy ${\mu }_r\approx 1$, vagyis $\mu ={\mu }_0\cdot {\mu }_r={\mu }_0$, így nem követünk el nagy hibát, ha a fenti differenciálegyenletet az alábbi alakban tárgyaljuk:

$\mathrm{\Delta }\overrightarrow{E}-\frac{n^2}{c^2}\frac{{\partial }^2\overrightarrow{E}}{\partial t^2}={\mu }_0\frac{{\partial }^2{\overrightarrow{P}}_{NL}}{\partial t^2}$,

Nemlineáris optikai jelenségek

Másodrendű jelenségek

• Összegfrekvencia-keltés

Abban az esetben, ha a közegbe ${\omega }_1$ és ${\omega }_2$ frekvenciájú fény lép és ${\omega }_3={\omega }_1+{\omega }_2$ frekvenciájú fény keletkezik, összegfrekvencia-keltésről beszélünk. Ennek egy speciális esete az ${\omega }_1={\omega }_2$; ilyenkor másodharmonikus keltésről, vagy frekvenciakétszerezésről beszélünk (a képen a b ábra szemlélteti ezt).

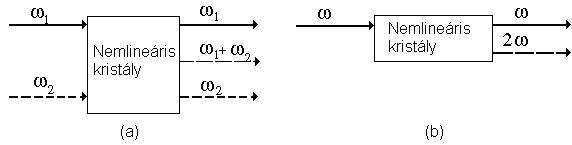
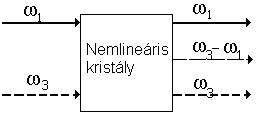
• Különbségfrekvencia-keltés

Különbségfrekvencia-keltésről beszélünk, ha a közegbe ${\omega }_1$ és ${\omega }_3$ frekvenciájú fény lép be, és egy ${\omega }_2={\omega }_3-{\omega }_1$ frekvenciájú is kilép a másik kettő mellett.

• Optikai parametrikus erősítés (OPA)

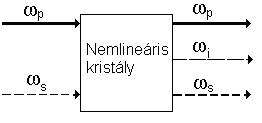
Amennyiben különbségfrekvencia-keltésnél az ${\omega }_3$ frekvenciakomponensű fény intenzitása számottevően nagyobb ${\omega }_1$ frekvenciakomponensűnél, valamint ${\omega }_2$ frekvenciakomponensű fény keletkezése mellett ${\omega }_1$ intenzitása jelentősen nő, optikai parametrikus erősítésről beszélünk. Ezen elven működő berendezés az optikai parametrikus erősítő (OPA – optical parametric amplifier). Ebben az esetben a legnagyobb intenzitású bemenő komponenst pumpálásnak (pump), az erősített komponenst jelnek (sign), a keletkezőt pedig idler-nek nevezzük. Ezen jelenségen alapul például az optikai parametrikus oszcillátor (OPO) működési elve.

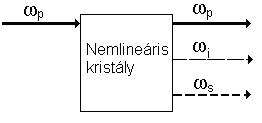
• Optikai parametrikus generálás (OPG)

Abban az esetben, ha a pumpálás elég nagy intenzitású, előfordulhat az az eset is, hogy a jel jelenléte nélkül is lezajlik egy, az előbb említett folyamathoz hasonló jelenség. Ebben az esetben optikai parametrikus generálásról (OPG – optical parametric generator) beszélünk.