Tétel: A háromszög köré írt kör tetszőleges pontjának az oldalegyenesekre eső merőleges vetületei egy egyenesbe esnek, ez az egyenes a Simson-egyenes.
Bizonyítás:
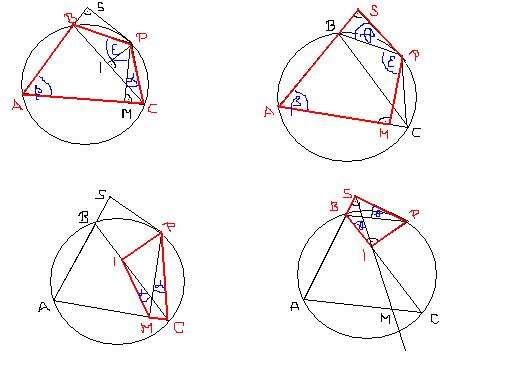 húrnégyszög .
húrnégyszög (-nél és -nél lévő szögei derékszögek) .
húrnégyszög, mert ( derékszögű) .
húrnégyszög (, -nél fekvő szögek derékszögűek) ; derékszögű: (két oldal és közbezárt szög – váltószögek) a többi szög is azonos.
(váltószögek), így egy egyenesbe esnek az , , pontok.
húrnégyszög .
húrnégyszög (-nél és -nél lévő szögei derékszögek) .
húrnégyszög, mert ( derékszögű) .
húrnégyszög (, -nél fekvő szögek derékszögűek) ; derékszögű: (két oldal és közbezárt szög – váltószögek) a többi szög is azonos.
(váltószögek), így egy egyenesbe esnek az , , pontok.
Külső hivatkozások
