Hegymászóprobléma

Példa a probléma megoldására

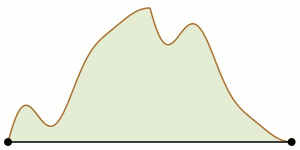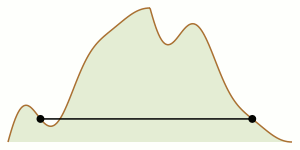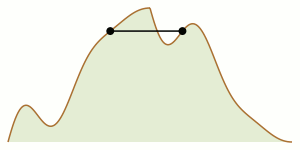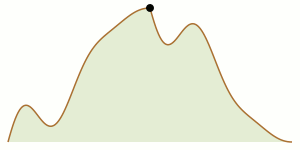
A matematikában hegymászóprobléma (mountain climbing problem) alatt azoknak a feltételeknek a megismerését értjük, melyet egy hegy kétdimenziós profiljának két oldalát meghatározó két függvénynek eleget kell tennie ahhoz, hogy két hegymászó a hegy két oldalán a csúcs felé elindulva, mozgásukat koordinálva úgy találkozhassanak (akár a hegy csúcsán), hogy végig azonos magasságon maradnak. A problémát ebben a formában James V. Whittaker (1966) vetette fel, nevét is tőle kapta, de története Tatsuo Homma (1952)-ig nyúlik vissza, aki egy változatát megoldotta. A problémát különböző kontextusokban újra és újra felfedezték és megoldották (ahogy az a jegyzetekben olvasható). Az 1990-es évektől kezdve előreléptek a probléma megértésében: összekötötték a sík görbéinek gyenge Fréchet-távolságával, a számítási geometria több mozgástervezési problémájával, a beírt négyzet problémájával, polinomok félcsoportjával stb. A problémát (Goodman, Pach & Yap 1989) cikke ismertette meg a szélesebb matematikakedvelő közönséggel, amiért 1990-ben elnyerték a Mathematical Association of America Lester R. Ford-díját.

A probléma lényege

A hegymászók mozgása könnyen koordinálható a csúcsok és völgyek (helyi maximumok és minimumok) között. A nehézséget az adja, hogy a haladáshoz a hegymászóknak időnként lefelé kell indulni a hegyről – néha az egyiknek, néha a másiknak, néha mindkettőnek. Hasonlóan, időről időre a mászók valamelyikének a kiindulási pontja felé vissza kell haladnia. Sőt, mint az megfigyelték, egy n csúccsal és völggyel rendelkező hegynél a visszafordulások száma n-nek akár négyzetes függvénye is lehet. Ezek a komplikációk a problémát intuitívan kevéssé átláthatóvá és néha egészen bonyolulttá teszik, elméletben és a gyakorlatban is.

Precíz megfogalmazás

(Huneke 1969) a következőt bizonyította:

Tegyük fel, hogy $f$ és $g$ folytonos függvények $[0,1]$ értelmezési tartománnyal és $[0,1]$ értékkészlettel, ahol $f(0)=g(0)=0$ és $f(1)=g(1)=1$, és egyik függvény sem állandó egyik intervallumon sem. Ekkor létezik az $s$ és $t$ folytonos függvény, mindkettő $[0,1]$ értelmezési tartománnyal és $[0,1]$ értékkészlettel, ahol $s(0)=t(0)=0$, $s(1)=t(1)=1$, és melyekre $f\circ s=g\circ t$, ahol „$\circ$” a függvénykompozíció jelölése.

Másrészről, Huneke eredménye nyilvánvalóan nem általánosítható tetszőleges folytonos függvényre. Ha ugyanis $f$ egy intervallumon konstans értéket vesz föl, míg $g$ végtelen sokszor oszcillál egy magasság körül, akkor az első mászónak végtelen sokszor kell előre-hátra haladnia, így soha nem érve fel a csúcsra. A szakaszosan lineáris esetnél nincsenek ilyen korlátozások. Ekkor a hegymászók mindig képesek úgy koordinálni a haladásukat, hogy felérjenek a csúcsra, tekintet nélkül arra, hogy vannak-e konstans magasságú intervallumok.

A szakaszosan lineáris eset bizonyítása

Tegyük föl, hogy mindkét függvény szakaszosan lineáris és nem tartalmaznak konstans magasságú intervallumot (fennsíkot). Vegyük az összes olyan $(x,y)$ páros halmazát, hogy ha az első mászó $x$-ben, a második $y$-ban található, akkor azonos magasságon vannak. Ha ezeket a pontpárokat a sík pontjai Descartes-koordinátaiként értelmezzük, akkor a halmaz szakaszok uniójából áll. Felfogható egy olyan $G$ irányítatlan gráf lerajzolásaként, melynek minden csúcsa egy szakasz végpontjának vagy egy metszéspontnak, az élek pedig két csúcsot összekötő szakasznak felelnek meg. Ez a gráf nem feltétlenül összefüggő. Különböző fajta csúcsai lehetnek:

• A $(0,0)$ csúcs fokszáma (az illeszkedő élek száma) egy: a két mászó csak egy irányba indulhat, fölfelé. Hasonlóan, az $(1,1)$ helyen a fokszám egy, mivel a mászók csak lefelé mehetnek.
• Ahol egyik mászó sincs se völgyben, se hegycsúcson, a fokszám kettő: elindulhatnak mindketten lefelé, vagy mindketten fölfelé.
• Ha az egyik mászó hegycsúcson vagy völgyben van, a másik pedig nem, a fokszám megintcsak kettő: a hegycsúcson vagy völgyben lévő mászó csak egyetlen irányba indulhat, a másiknak pedig követnie kell őt.
• Ahol mindkét mászó hegycsúcson van, vagy mindkét mászó völgyben, négy a fokszám: mindkét mászó egymástól függetlenül eldöntheti, merre induljon.
• A $G$-t meghatározó $(x,y)$ csúcspárok között előfordulhatnak olyanok, ahol az egyik mászó hegycsúcson, a másik völgyben van. Ezek a pontok a $G$ izolált csúcsaiként értelmezhetők: egyik mászó sem tud mozdulni, a fokszám tehát nulla.

A kézfogás-lemma szerint egy irányítatlan gráf minden összefüggő komponense páros számú páratlan fokszámú csúcsot tartalmaz. Mivel kizárólag a $(0,0)$ és az $(1,1)$ csúcs fokszáma páratlan, ennek a két csúcsnak ugyanabba az összefüggő komponensbe kell tartozniuk. Ezért $G$-ben léteznie kell $(0,0)$-ból $(1,1)$-be vezető útnak. Hegymászónyelvre lefordítva, a gráfban ez az út megmutatja, hogyan koordinálhatják a mászók mozgásukat a hegycsúcsig. A szakaszonként lineáris, de fennsíkokat (konstans magasságú intervallumot) is tartalmazó eset bizonyítása a fentihez hasonló, de kissé bonyolultabb esetvizsgálatot tartalmaz. Alternatívaként előállítható az olyan módosított függvényekhez tartozó út, melyben az állandó magasságú intervallumok egy-egy pontba sűrűsödnek, majd ez az út kiterjeszthető az eredeti függvényekre.

Fordítás

Ez a szócikk részben vagy egészben a Mountain climbing problem című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

• Baird, B. B. & Magill, K. D., Jr. (1997), "Green's ${ℛ}$, ${𝒟}$ and ${\mathscr{H}}$ relations for generalized polynomials", Semigroup Forum 55 (3): 267–293, DOI 10.1007/PL00005929.
• Buchin, Kevin; Buchin, Maike & Knauer, Christian et al. (2007), "How difficult is it to walk the dog?", Proc. 23rd European Workshop on Computational Geometry (Graz, 2007), pp. 170–173.
• Goodman, Jacob E.; Pach, János & Yap, Chee-K. (1989), "Mountain climbing, ladder moving, and the ring-width of a polygon", American Mathematical Monthly 96 (6): 494–510, doi:10.2307/2323971, <http://www.maa.org/sites/default/files/pdf/upload_library/22/Ford/Goodman-Pach-Yap494-510.pdf>.
• Homma, Tatsuo (1952), "A theorem on continuous functions", Kōdai Mathematical Seminar Reports 4: 13–16, DOI 10.2996/kmj/1138843207.
• Huneke, John Philip (1969), "Mountain climbing", Transactions of the American Mathematical Society 139: 383–391, DOI 10.2307/1995331.
• Jiménez López, Víctor (1999), "An elementary solution to the mountain climbers' problem", Aequationes Mathematicae 57 (1): 45–49, DOI 10.1007/s000100050069.
• Keleti, Tamás (1993), "The mountain climbers' problem", Proceedings of the American Mathematical Society 117 (1): 89–97, DOI 10.2307/2159702.
• Lipiński, J. S. (1957), "Sur l'uniformisation des fonctions continues", Bull. Acad. Polon. Sci. Cl. III 5: 1019–1021, LXXXV.
• McKiernan, M. A. (1985), "Mountain climbing: an alternate proof", Aequationes Mathematicae 28 (1-2): 132–134, DOI 10.1007/BF02189402.
• Mioduszewski, J. (1962), "On a quasi-ordering in the class of continuous mappings of a closed interval into itself", Colloquium Mathematicum 9: 233–240.
• Pak, Igor (2010), Lectures on Discrete and Polyhedral Geometry, p. 39, <http://www.math.ucla.edu/~pak/book.htm>.
• Sikorski, R. & Zarankiewicz, K. (1955), "On uniformization of functions. I", Fundamenta Mathematicae 41: 339–344.
• Tucker, Alan (1995), "The parallel climbers puzzle", Math Horizons 3 (2): 22–24, <http://www.maa.org/sites/default/files/pdf/upload_library/22/Evans/november_1995_22.pdf>.
• Whittaker, James V. (1966), "A mountain-climbing problem", Canadian Journal of Mathematics 18: 873–882, DOI 10.4153/CJM-1966-087-x..

További információk

• The Parallel Mountain Climbers Problem, a description and a Java applet solution.