Ortonormált bázis

Legyen $V$ vektortér, amelyen definiálva van egy skaláris szorzat (azaz egy $⟨.,.⟩:V\times V\to \mathbb{ℝ}$ szimmetrikus, bilineáris, pozitív definit függvény). Az $e_1,...,e_n$ vektorrendszert $V$ ortonormált bázisának nevezzük, ha minimális generátorrendszer $V$-ben, minden vektora egység hosszúságú és bármely két vektora egymásra merőleges, ami azt jelenti, hogy skalárszorzatuk nulla. Ortonormált bázis konstruálható például úgy, hogy a Gram–Schmidt-eljárás segítségével ortogonális bázist konstruálunk, majd minden $b_i$ bázisvektort elosztunk $\sqrt{⟨b_i,b_i⟩}$-vel. Az ortonormált bázis véges és végtelen esetben is értelmezhető.

Véges dimenzióban

A következőkben legyen $V$ véges dimenziós, skalárszorzattal ellátott vektortér, vagyis valós vagy komplex vektortér, az $⟨\cdot ,\cdot ⟩$ skalárszorzattal. Komplex esetben feltesszük, hogy a skalárszorzat lineáris a második argumentumában, és szemilineáris az elsőben, tehát

$\lambda ⟨v,w⟩=⟨\overline{\lambda }v,w⟩=⟨v,\lambda w⟩$

minden $v,w\in V$ vektorra és minden $\lambda \in \mathbb{ℂ}$-re. A skalárszorzat az $\Vert \cdot \Vert =\sqrt{⟨\cdot ,\cdot ⟩}$ normát indukálja.

Definíció és létezés

Egy $n$-dimenziós, skalárszorzattal ellátott $V$ vektortér ortonormált bázisa egy $B=\{b_1,\dots ,b_n\}$ ortornormált rendszer, ami a következőket jelenti:

• Minden vektor hossza egységnyi,

  $\Vert b_i\Vert =\sqrt{⟨b_i,b_i⟩}=1$ minden $i\in \{1,\dots ,n\}$ esetén

• A vektorok páronként ortogonálisak,

  $⟨b_i,b_j⟩=0$ minden $i,j\in \{1,\dots ,n\}$ esetén, ahol $i\ne j$.

Minden véges dimenziós skalárszorzatos vektortérnek van ortonormált bázisa. A tér minden bázisa Gram–Schmidt ortogonalizációval és normálással ortonormált bázissá alakítható. Mivel az ortonormált rendszerek lineárisan függetlenek, azért egy $n$-dimenziós skalárszorzatos vektortérben $n$ ortonormált vektorból álló rendszer ortonormált bázist alkot.

A bázis kezessége

Adva legyen a $V$ vektortérnek egy $B=(b_1,\dots ,b_n)$ rendezett ortonormált bázisa. Alkossuk meg a

$Q=\left(\begin{array}{cccc}{b}_1& b_2& \dots & b_n\end{array}\right)$

mátrixot a bázis vektoraiból, mint oszlopokból! Valós vektorterekben egy ilyen mátrix determinánsa 1 vagy -1. Ha $\det (Q)=+1$, akkor $b_1,\dots ,b_n$ jobbrendszer, különben balrendszer.

Példák

Az $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ ortonormált bázis ${\mathbb{ℝ}}^3$-ben, és egy velük ábrázolt $\overrightarrow{r}=3\overrightarrow{i}+2\overrightarrow{j}+3\overrightarrow{k}$ vektor

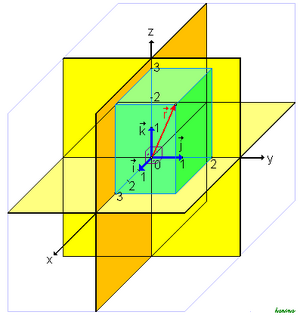
Az ${\mathbb{ℝ}}^3$ tér standard bázisa, az

$$\begin{gathered} \overrightarrow{i}={\overrightarrow{e}}_1=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right), \\ \overrightarrow{j}={\overrightarrow{e}}_2=\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right), \\ \overrightarrow{k}={\overrightarrow{e}}_3=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right), \end{gathered}$$

vektorokkal, az ${\mathbb{ℝ}}^3$ standard skalárszorzattal ellátott vektortér ortonormált bázisa. Bázis ${\mathbb{ℝ}}^3$-ben, minden vektor hossza 1, és páronként merőlegesek, mivel páronkénti skalárszorzatuk nulla. Általában, egy ${\mathbb{ℝ}}^n$ illetve ${\mathbb{ℂ}}^n$, standard skalárszorzattal ellátott koordinátatérben az $\{e_1,\dots ,e_n\}$ standard bázis ortonormált bázis. ${\mathbb{ℝ}}^2$-ben a

${\overrightarrow{b}}_1=\left(\begin{array}{c}\frac{3}{5}\\ \frac{4}{5}\end{array}\right)$   és   ${\overrightarrow{b}}_2=\left(\begin{array}{c}-\frac{4}{5}\\ \frac{3}{5}\end{array}\right)$

vektorok ortonormált rendszert alkotnak a standard skalárszorzat szerint, így ${\mathbb{ℝ}}^2$ egy ortonormált bázisa.

Koordinátaábrázolások

Vektorok

Ha $B=\{b_1,\dots ,b_n\}$ ortonormált bázis $V$-ben, akkor egy $v\in V$ vektor koordinátái ortogonális projekcióval számíthatók. Ha $v$ ábrázolása a $B$ bázisban

$v=v_1{b}_1+\dots +v_n{b}_n=\sum _{i=1}^n{v}_i{b}_i,$

akkor

$v_i=⟨b_i,v⟩$, $i=1,\dots ,n$

és

$⟨b_i,v⟩=⟨b_i,\sum _{j=1}^n{b}_j{v}_j⟩=\sum _{j=1}^n⟨b_i,b_j{v}_j⟩=\sum _{j=1}^n⟨b_i,b_j⟩v_j=\sum _{\genfrac{}{}{0ex}{}{j=1}{j\ne i}}^n\underset{0}{\underbrace{⟨b_i,b_j⟩}}{v}_j+⟨b_i,b_i⟩v_i=v_i$

ezzel

$v=\sum _{i=1}^n⟨b_i,v⟩b_i.$

A fenti 2. példában az $\overrightarrow{v}=\left(\begin{array}{c}2\\ 7\end{array}\right)$ vektorra:

$⟨{\overrightarrow{b}}_1,\overrightarrow{v}⟩=\frac{3}{5}\cdot 2+\frac{4}{5}\cdot 7=\frac{34}{5}$   és

$⟨{\overrightarrow{b}}_2,\overrightarrow{v}⟩=-\frac{4}{5}\cdot 2+\frac{3}{5}\cdot 7=\frac{13}{5}$

így pedig

$\overrightarrow{v}=\frac{34}{5}{\overrightarrow{b}}_1+\frac{13}{5}{\overrightarrow{b}}_2=\frac{34}{5}\left(\begin{array}{c}\frac{3}{5}\\ \frac{4}{5}\end{array}\right)+\frac{13}{5}\left(\begin{array}{c}-\frac{4}{5}\\ \frac{3}{5}\end{array}\right).$

Skalárszorzat

Egy ortonormált bázisban a bázisbeli koordinátákból a hozzá tartozó skalárszorzat standard skalárszorzatként számítható. Bővebben: Ha $B=\{b_1,\dots ,b_n\}$ ortonormált bázis $V$-ben, és a $v$ és $w$ vektorok koordináta-ábrázolása $B$-ben $v=v_1{b}_1+\dots +v_n{b}_n$ és $w=w_1{b}_1+\dots +w_n{b}_n$, so gilt

$⟨v,w⟩=v_1{w}_1+\dots +v_n{w}_n$

valós, illetve

$⟨v,w⟩={\overline{v}}_1{w}_1+\dots +{\overline{v}}_n{w}_n$

komplex esetben.

Ortogonális leképezések

Ha $f:V\to V$ valós esetben ortogonális, komplex esetben unitér leképezés, és $B$ ortonormált bázis $V$-ben, akkor $f$ a $B$ bázisban ortogonális, illetve unitér mátrixszal ábrázolható. Más bázisokra ez az állítás nem igaz.

Végtelen dimenzióban

Definíció

Legyen $(V,⟨\cdot ,\cdot ⟩)$ prehilberttér, és legyen $\Vert \cdot \Vert =\sqrt{⟨\cdot ,\cdot ⟩}$ a skalárszorzat által indukált norma. Egy $S\subset V$ részhalmaz ortonormált rendszer, ha $\Vert e\Vert =1$ és $⟨e,f⟩=0$ minden $e,f\in S$ párra, ahol $e\ne f$. Egy ortonormált rendszer, melynek lineáris burka sűrű a térben, a tér ortonormált bázisa vagy Hilbert-bázisa. Megjegyezzük, hogy ellentétben a véges dimenzióval egy ortonormált bázis nem Hamel-bázis, vagyis nem bázis lineáris algebrai értelemben. Ez azt jelenti, hogy $V$ nem minden eleme fejezhető ki $S$ véges sok elemének lineáris kombinációjaként. Viszont előáll megszámlálhatóan végtelen elem lineáris kombinációjaként, vagyis feltétlenül konvergens sorként. Egy $S=(e_n{)}_{n\in \mathbb{\mathbb{N}}}$ ortonormált rendszer teljes, ha minden $x\in V$ elemre

$\underset{n\to \mathrm{\infty }}{\lim }\Vert x-\sum _{k=0}^n⟨x,e_k⟩e_k\Vert =0$.

Jellemzés

Egy $H$ prehilberttér esetén a következők ekvivalensek:

• $S\subset H$ ortonormált bázis
• $S$ ortonormált rendszer és teljesül a Parseval-formula:

$\Vert x{\Vert }^2=\sum _{v\in S}|⟨x,v⟩{|}^2$ minden $x\in H$.

Ha $H$ még teljes is, tehát Hilbert-tér, akkor ekvivalens is:

• Az $S$ $S^{\perp }$ ortogonális komplementere a nulltér, mivel általában egy $T$ részhalmazra ${T^{\perp }}^{\perp }=\overline{\mathrm{span}(T)}$.
• Konkrétabban, pontosan akkor teljesül, hogy $x=0$, ha minden $v\in S$ esetén $⟨x,v⟩=0$
• Ha $S$ az inklúzióra maximális ortonormált rendszer, vagyis minden $S$-t tartalmazó ortonormált rendszer megegyezik $S$-sel. Ha egy $S$ ortonormált rendszer nem maximális, akkor lenne egy nullától különböző vektor az ortogonális komplementerben, melyet lenormálva hozzávehetnénk a rendszerhez. Ezzel szintén ortonormált rendszert kapunk, ami szigorúan bővebb, mint az eredeti.

Létezés

A Zorn-lemmával megmutatható, hogy minden $H$ Hilbert-térnek van ortonormált bázisa. Tekintsük $H$-ban az összes ortonormált rendszert, rendezve a tartalmazásra. Ez nem üres, mivel az üres halmaz is ortonormált rendszer. Ortonormált rendszerek minden felszálló lánca a tartalmazásra nézve felülről zárt, különben az egyesítés nem adna ortonormált rendszert. Lenne egy vektor, ami nem normált, vagy tartalmazna két nem ortogonális vektort, melyeket valamelyik egyesített ortonormált rendszernek már tartalmaznia kell. Ezért a Zorn-lemma miatt létezik maximális ortonormált rendszer, egy ortonormált bázis. Az összes ortonormált rendszer helyett tekinthetjük azokat, amelyek egy adott ortonormált rendszert tartalmaznak. Hasonlóan kapjuk, hogy minden ortonormált rendszer kiegészíthető ortonormált bázissá. Alternatívan, alkalmazható a Gram–Schmidt-ortogonalizáció a teljes $H$-ra vagy egy sűrű részhalmazára. Ezzel is ortonormált bázishoz jutunk. Minden szeparábilis prehilberttérnek van ortonormált bázisa. Válasszunk egy (legalább) megszámlálható sűrű részhalmazt, és alkalmazzuk a Gram–Schmidt-ortogonalizációt. Most nincs szükség a teljességre, mivel csak véges dimenziós alterekre vetítenek, melyek mindig teljesek. Ezzel (legfeljebb) megszámlálható ortonormált bázist kapunk. Megfordítva, minden prehilberttér, aminek van (legfeljebb) megszámlálható ortonormált bázisa, szeparábilis.

Sorfejtés ortonormált bázis szerint

Egy $S$ ortonormált bázisú $(H,⟨\cdot ,\cdot ⟩)$ Hilbert-térnek megvan az a tulajdonsága, hogy minden $v\in H$ ábrázolható, mint

$v=\sum _{u\in S}⟨u,v⟩u$

Ez a sor feltétlenül konvergens. Ha a Hilbert-tér véges dimenziós, akkor a feltétlen konvergencia egybeesik az abszolút konvergenciával. Ez a sor az általánosított Fourier-sor. Ha ugyanis a négyzetesen konvergens valós értékű függvények $L^2([0,2\pi ])$ Hilbert-terét választjuk, és ellátjuk az

$⟨f,g⟩=\underset{0}{\overset{2\pi }{\int }}f(x)g(x)\mathrm{d}x,$

skalárszorzattal, akkor

$S=\{c_0\}\cup \{c_n,s_n\mid n\in \mathbb{\mathbb{N}}\}$

ahol

$$\begin{gathered} c_0(x)=\frac{1}{\sqrt{2\pi }}, \\ {c}_n(x)=\frac{1}{\sqrt{\pi }}\cos (nx), \\ {s}_n(x)=\frac{1}{\sqrt{\pi }}\sin (nx) \end{gathered}$$ minden $x\in [0,2\pi ]$ és $n\in \mathbb{\mathbb{N}}$ esetén.

ortonormált bázis $L^2([0,2\pi ])$-ben. Ebben a bázisban $⟨f,c_0⟩=\frac{1}{\sqrt{2\pi }}\underset{0}{\overset{2\pi }{\int }}f(x)\mathrm{d}x,$

$⟨f,c_n⟩=\frac{1}{\sqrt{\pi }}\underset{0}{\overset{2\pi }{\int }}f(x)\cos (nx)\mathrm{d}x$

és

$⟨f,s_n⟩=\frac{1}{\sqrt{\pi }}\underset{0}{\overset{2\pi }{\int }}f(x)\sin (nx)\mathrm{d}x,n\in \mathbb{\mathbb{N}}$

éppen $f$ Fourier-sorának Fourier-együtthatói. Ezzel a Fourier-sor éppen az $L^2([0,2\pi ])$ elemének sorábrázolása az adott ortonormált bázisban.

További példák

Legyen ${\ell }^2$ a négyzetesen összegezhető sorozatok sorozattere. Az $S=\{e_n:n\in \mathbb{\mathbb{N}}\}$ halmaz ortonormált bázisa ${\ell }^2$-nek.

Források

• Freud Róbert, Lineáris algebra, ELTE Eötvös Kiadó, 1998.
• Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-03217-0.
• Dirk Werner: Funktionalanalysis. 6., korrigierte Auflage. Springer-Verlag, Berlin 2007, ISBN 978-3-540-72533-6, S. 222–236.

Fordítás

Ez a szócikk részben vagy egészben az Orthonormalbasis című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.